carchedi-roberts-inflation-presentation-finalDownload The purpose of this post is to ensure our understanding of Marxist categories remains precise and that all our investigations are rigorous.
OBSERVATIONS OF CARCHEDI & ROBERTS’ PRESENTATION ON INFLATION GIVEN AT THE RECENT HISTORICAL MATERIALISM CONFERENCE.
Tag: Materialismo Dialéctico
Historical Materialism Conference – monopoly, imperialism, inflation and Ukraine

As usual it won’t be possible to report on all the many sessions at this year’s London Historical Materialism conference that took place last weekend. I could only attend a few sessions and concentrated, naturally, on ones to do with Marxist economics. Also, I was participating in two sessions myself that clashed with others that […]
Historical Materialism Conference – monopoly, imperialism, inflation and Ukraine
UN COMENTARIO SOBRE “¿Formadores de precios o interdependencia?”
Una idea muy extendida en Argentina es que la elevada inflación se debe, en gran medida, a los “formadores de precios”. Se trataría de oligopolios que aumentan “de manera unilateral” los precios de sus productos, desatando una cadena de subas en cascada en el resto de la economía. La “unilateralidad” en el establecimiento de esos […]
¿Formadores de precios o interdependencia?
Más allá de la interesante curiosidad de que alguien que no considera válido el teorema fundamental de la economía política marxista (la ley de la tendencia decreciente de la tasa media de ganancia) acuda a los fundamentos del Marxismo para refutar la idea de la existencia del poder de monopolio, un error gnoseológico fundamental que exhibe el artículo en cuestión es olvidar, como a menudo los economistas “marxistas” lo hacen, de que si bien la inflación tiene su fundamento último en el sector real, no es menos cierto que el poder económico que les procura a los grandes capitalistas su dominancia en el sector real se transmite al sector financiero por cuanto estos sectores están íntimamente vinculados (con dominancia, en última instancia, del sector real sobre el sector financiero -y los cracks bursátiles son, precisamente, el mecanismo mediante el cual los sistemas de economía política corrigen la violación al postulado anterior-), así como tampoco es menos cierto que la ciencia en cuestión no se llama economía (ni siquiera los amos y amas de casa hacemos economía, porque siempre hay relaciones de poder, en una sociedad de clases, inherentes a todo fenómeno de distribución del ingreso -probablemente en las tribus del Amazonía es diferente-), sino economía política y en tal sentido posee la implicación de relaciones de poder, de relaciones de dominantes y dominados que expresan una determinada estructura de clases que se corresponde a un determinado grado de desarrollo de las fuerzas productivas del trabajo, relaciones de poder que son también técnicas, puesto que lo político es un fenómeno exclusivo de las sociedades humanas y, por consiguiente, un fenómeno de estudio de las ciencias sociales, y como tal posee inherentemente una explicación científica, íntimamente ligada a la de los fenómenos económicos, de ahí que la ciencia se llame, insisto, economía política.
El mismo articulista, en otro artículo, ha planteado la interesante hipótesis de que la inflación ocurre para que las innovaciones tecnológicas repercutan en la tasa media de ganancia, es decir, para que se materialice la plusvalía relativa. Más allá de que la hipótesis en cuestión sea planteada en un escenario de valores y no de precios de producción, además del hecho de que Rosdolsky ha señalado (fundamentalmente en el apartado relativo a los salarios reales dentro de su estudio de los Grundrisse) que la caída de los salarios reales no es una tendencia generalizada a escala planetaria (o alza, en el caso que la innovación no provenga de las ramas productivas que producen mercancías que componen la canasta salarial, al menos durante el período de rezago de la transmisión de la innovación a las ramas productivas que componen la canasta en cuestión), es razonable esperar que el escenario de precios de producción simplemente complejice y/o complique el mecanismo mediante el cual la relación entre la plusvalía relativa y la inflación se expresa, así como también que se pueda justificar que en los países desarrollados los salarios reales no caigan en términos del mecanismo mediante el cual ocurre un proceso de nivelación tendencial a nivel mundial de los salarios (en la primera página del capítulo VIII del tomo III de El Capital, en la antesala a su planteamiento sobre el surgimiento de los precios de producción -capítulo IX de la misma fuente antes referida-), específicamente explicando que en los grandes centros industriales los salarios reales no decaen porque las ganancias de los capitalistas de estos centros, mermadas por tal efecto, son compensadas por las ganancias que estos mismos capitalistas obtienen de sus inversiones en los países de la perisferia (perisferias de tales centros). Sin embargo, lo curioso del planteamiento del articulista es que en tal artículo se dice explícitamente que para que esto ocurra los bancos centrales deben garantizar un determinado nivel de inflación (y se hace alusión a la “regla de Taylor” que siguen muchos bancos centrales -con independencia que no es el único régimen monetario existente en los países capitalistas y que los planteamientos en cuestión deberán ser generalizados considerando esos otros regímenes monetarios-). Más allá que el articulista no explica los criterios técnicos bajo los cuales los bancos centrales fijan determinada tasa de inflación a la luz de su hipótesis de la innovación tecnológica como causa fundamental de la inflación (lo cual es fundamental para que la hipótesis se sostenga), cualquier persona que tenga conocimiento práctico y objetivo de cómo se trabaja al interior de los bancos centrales (a nivel de los economistas jefe, gerencia, presidencia y junta directiva) sabe que muchas políticas monetarias se toman en tales instituciones bajo el único criterio de procurarles mayores ganancias a los grandes capitalistas (por ejemplo, las devaluaciones cambiarias que ocurren en muchos países -como parte de una política cambiaria- en determinados momentos del año, como en el caso particular del escenario en que ocurre una depreciación del dólar estadounidense, los bancos privados en determinados países tienen sus posiciones dolarizadas y el banco central devalúa la moneda nacional para que las ganancias de los bancos privados no se vean afectadas -y en muchos casos aumenten-), sin que existan de por medio, ni siquiera por asomo, el riesgo de que por no realizarse tal política monetaria las condiciones de reproducción del proceso de acumulación de capital se rompan y la economía pueda entrar en crisis, o que en ausencia de tales políticas monetarias los inversionitas decidiecen abandonar el país, etc., es decir, sin que exista ningún fundamento técnico-económico de por medio, aunque sí un fundamento técnico-político. Insistimos, por ello se llama economía política y no meramente economía. Esto no significa que la hipótesis planteada por el articulista citado sobre la naturaleza tecnológica (y, por consiguiente, real) de la inflación no pueda ser el elemento central (de hecho, el elemento central de la inflación es una cuestión técnica-económica proveniente del sector real, sea a través de la hipótesis citada o de otra hipótesis de la misma naturaleza), sino que no es lo único que constituye el fenómeno en cuestión, por el contrario, tal fenómeno tiene dos aristas, ambas totalmente materiales y objetivas (en donde la política está supeditada a la económica por cuanto las relaciones de clase existen en cuanto al interior del proceso de producción existe una distinta vinculación con los medios de producción por parte de dos sectores de la sociedad humana), ambas regidas por criterios científico-técnicos.
Esto me recuerda a aquella célebre frase de Lenin, citada por Rosdolsky, que describía cómo los “marxistas”, a causa de no leer a Hegel, seguían (para aquella época) sin entender a Marx, cuestión que sigue siendo válida para los “marxistas” de hoy en día (e incluso de los anteriores a Lenin, célebre es también la frase de Marx de “Si estos son marxistas, yo no soy marxista”), especialmente para los economistas. La lógica dialéctica-materialista no es una lógica dicotómica, es decir, no es del tipo “o es una relación regulada rigurosamente por un criterio técnico-económico o es subjetivismo”, por cuanto la base económica y la superestructura ideológica están íntimamente ligadas (supeditándose la superestructura, en última instancia, a la base), tanto como lo está lo económico a lo político, puesto que un sistema económico de clases (de economía política) no puede subsistir sin una dictadura, es decir, sin que una clase A (la dominante) imponga a otra clase B (la dominada) sus intereses (intereses que son antagónicos entre sí) con independencia del medio usado para ello, porque aunque la independencia antes expresada exista, lo ideológico (expresado como alienación, concepto teórico que Marx desarrolla en los Manuscritos Económicos y Filosóficos de 1844) es el elemento indispensable para garantizar la existencia fáctica de la dictadura (en dictaduras militares, es decir, en dictaduras formales, evidentemente lo ideológico juega un papel menos preponderante -no por ello deja de ser preponderante, porque al fin y al cabo la rebelión contra las dictaduras militares es, en la enorme mayoría de casos, contra la no-inclusión política, no contra la estructura distributiva y menos contra las relaciones sociales de producción-, mientras que en dictaduras fácticas -las democracias burguesas- lo ideológico cobra aún más relevancia), por lo que existe una retroalimentación entre la base económica y la superestructura ideológica, en cuanto la ideología sólo son las condiciones materiales de existencia (la existencia se define como lo que es, lo que no es, lo que será, lo que no será, lo probable, lo posible y lo lógico) de períodos de tiempo pasados cristalizadas en el presente, bajo determinada teleología (causa final, finalidad, que en sociedades de clase, para el caso de la ideología dominante -que es la ideología que en promedio permea la sociedad-, es la alienación), en la cabeza de los individuos. No por ello significa que la superestructura no esté sometida, en última instancia, a la base económica, así como existe una retroalimentación de la misma índole entre la fuerza de trabajo y los medios de producción (siendo estos últimos crisálidas en el tiempo de la primera) y no por ello Marx afirmó que el capital podía crear valor, sino todo lo contrario como es (o debería ser) ampliamente conocido. Que la propiedad privada, tal como Marx replicó a Proudhon, no sea un robo sino una necesidad histórica, no significa que no puedan operarse robos a través de ella (entendiendo estos como apropiaciones de trabajo ajeno que no obedecen rigurosamente a necesidades de acumulación -es decir, sin las cuales las condiciones de reproducción se romperían-, sino que obedecen a motivos subjetivos del capitalista, explicados estos a su vez de forma objetiva por la psicología que genera la categoría económica que los capitalistas personifican, que imprime en ellos la necesidad de ser voraces, codiciosos y ambiciosos; puesto que la ética es parte de la superestructura y esta ya se definió en términos objetivos, materiales y temporales, no existe contradicción entre esta afirmación y lo antes expuesto). ¿Acaso el violento, mugriento y sangriento proceso de acumulación originaria de capital descrito por Marx (que no sólo ocurrió en Europa, también en toda América Latina, aunque con una fenomenología parcialmente diferente) no requiere de un sistema ético en la cabeza de los individuos que la llevaron a cabo?, ¿o es que acaso un consecuente y devoto monge franciscano, o un pacifista, podrían haber llevado a cabo un genocidio de tal índole y magnitud? Roma no terminó de ser Roma por las lanzas que llevaban sus legiones, sino por las ideas que esas legiones, con esas lanzas, imponían en la cabeza de los pueblos que conquistaban, más no por ello es menos cierto que esas lanzas existían gracias a las condiciones materiales de existencia del Imperio mismo.
Para que no quede duda de la afirmación anterior, el mismo articulista, que no se ruboriza al hablar de dialéctica sin citar a Hegel, ha expresado abiertamente en su blog (específicamente en respuesta a comentarios que yo esgrimí en una de sus publicaciones), que la ley de la tendencia decreciente de la tasa media de ganancia no es válida científicamente. Más allá que existen sobradas verificaciones empíricas de que esta tendencia es objetiva, verificaciones que no sólo provienen de escuelas marxistas que son antagónicas en su uso instrumental de las matemáticas (como la escuela temporalista y la escuela simultaneista, por ejemplo), sino también de macroeconometristas neoclásicos como Mankiw o Blanchard (este último fue economista jefe del Fondo Monetario Internacional, que representa la ortodoxia financiera a nivel institucional supranacional), afirmar eso es precisamente ser lego en lógica dialéctica; muchos economistas buscan emplear una lógica sublime (que termina siendo muchas cosas, menos sublime), pero olvidan que la realidad existe y que hay que “contaminarse” de ella. Lo anterior es así por cuanto la sociedad comunista sin clases es la teleología histórica-social de la humanidad desde la perspectiva de Marx y, para que ello se verifique, debe existir un fundamento material y objetivo de la inviabilidad a largo plazo del modo de producción capitalista, es precisamente este fundamento la ley de la tendencia decreciente de la tasa media de ganancia, ley que cualquier empresario que posea un cierto nivel mínimo de acumulación de capital y de elevada composición orgánica del mismo, comprende con total claridad. Esta ley, planteada por vez primera por Adam Smith (según el mismo Marx), no fue simplemente resultado observacional del comportamiento de los capitalistas en la época de Marx, tampoco fue simplemente el resultado de teorizar sobre los datos que Engels enviaba a Marx sobre la estructura y dinámica productiva de sus empréstitos fabriles (lo que puede ser verificado en la correspondencia entre ellos), tampoco fue una mera continuación de los postulados clásicos sobre dicha tendencia, es también el resultado lógico de la ingeniería inversa que Marx realiza al sistema hegeliano, por cuanto los valores (que en el sistema hegeliano son la esencia, esencia que Hegel retoma de Spinoza) son “diluidos” en un mecanismo (que Hegel crea sintetizando orgánicamente todos los sistemas filosóficos que le precedieron, especialmente el metafísico de Aristóteles, que es conciliado con los requerimientos instrumentales del sistema kantiano; para el caso del sistema económico capitalista es la competencia capitalista misma) en que la premisa se presenta depurada dialécticamente en el resultado (los precios de producción, para el caso del sistema económico capitalista). Establecido lo anterior (no sólo a nivel conceptual, sino a nivel de las estructuras matemáticas con que se representan), si la dinámica económica capitalista se estudia en presencia de perpetua innovación tecnológica (que es lo que ocurre en la realidad objetiva, por ejemplo, con el caso de los teléfonos inteligentes, por mostrar un ejemplo simple y cotidiano) es inexorable que la tasa media de ganancia del sistema caiga (capítulo XIII del tomo III de El Capital), aunque como también establecería Marx en los capítulos XIV y XV de la misma fuente citada, esta ley es contarrestada a causa del desarrollo de las contradicciones internas de los componentes integrantes. Los “marxistas” (a quienes es preciso, en términos gnoseológicos, mejor llamar neo-marxistas), no comprenden que el sistema de Marx, al igual que el sistema hegeliano, es “de una sola pieza” (indivisible, o conjunto conexo, como se conoce a ciertos sistemas de conjuntos en Matemáticas), puesto que la gran fortaleza del sistema de Marx es la unificación orgánica de la ontología (la doctrina del Ser), la lógica y la teoría del conocimiento, gnoseología o epistemología, de la misma forma en que en mecánica cuántica al hablar de “Momento” no se puede hablar del “Momento” de una de las fuerzas fundamentales de la Naturaleza, porque dentro de la integral a través de la cual se calcula dicho Momento, no es posible separar dentro de la función objetivo las fuerzas fundamentales a través de ella modelada, a diferencia de lo que ocurría en mecánica clásica en que sí es posible separar las fuerzas que actúan sobre un sistema físico (por ejemplo, una palanca). Esto expresa una ontología, una lógica y una gnoseología muy clara: que la Naturaleza es orgánica e indivisible a nivel de su esencia (entendiendo la esencia, al igual que Hegel, como el fundamento de la existencia), aunque por supuesto sea posible dividir las partículas que la componen a nivel local (y que incluso, como señaló Lenin en Materialismo y Empiriocriticismo, el potencial de esta división sea tendencialmente inagotable), puesto que si no fuese posible se incurriría en una visión leibniziana de la existencia, es decir, en una visión monista extrema. Se hace referencia a otro tipo de sistemas, porque cualquier persona que posee conocimientos básicos de dialéctica sabe que la misma es una metalógica multinivel recursiva hacia el pasado o, en términos más simples, que la verdad está en lo absoluto, en la totalidad.
Así, retomando lo relativo a las sociedades humanas, la teleología intra-histórica (a nivel de un modo de producción, en este caso el capitalista, que tiene como finalidad la acumulación, concentración y centralización de capital) se somete a la teleología inter-histórica, por cuanto el mismo proceso de acumulación de capital genera las condiciones para el derrumbe económico y político del capitalismo y el surgimiento, desde las mismas entrañas del capitalismo, de una nueva sociedad, de la sociedad comunista sin clases y con ello, como expresa Marx en el prólogo de Contribución a la Crítica de la Economía Política, se pondrá fin a la prehistoria de la humanidad y se dará comienzo a un nuevo ciclo de las sociedades humanas, superando el ciclo de las sociedades de clase (aunque este nuevo ciclo generado desde ellas, desde lo que se supera), generadas desde las sociedades sin clase (a causa de la precariedad tecnológica, lo cual se explica magistralmente en El Origen de la Familia, la Propiedad Privada y el Estado). Un mundo mejor es posible y no sólo es posible, sino que también se gestará y la lucha de clases será su partera, no como un hecho histórico que emanará esencialmente de la conciencia de los individuos, sino de la necesidad histórica (objetivas y materiales) de la sociedad humana en general (como establece Engels, la violencia es la partera de la Historia, lo cual ocurre también en física fundamental, por ejemplo, con el papel que los agujeros negros supermasivos al fondo de la galaxia desempeñan en las órbitras de los cuerpos celestes y estas últimas en el surgimiento de la vida, así como también a nivel más abstracto con los operadores de aniquilación halmitonianos de partículas), como la premisa que se presenta en el resultado de forma depurada y que determina dicho resultado, como una necesidad histórica que se cristalizará en la conciencia de los seres humanos cuando exista el suficiente grado de desarrollo de las fuerzas productivas del trabajo. En palabras de Marx, el monopolio feudal engendró la libre competencia capitalista, esta última engendró los monopolios capitalistas y, así, se establecen gradual y progresivamente (no sin retrocesos, puesto que la evolución dialéctica de la existencia en general y en particular ocurre a manera de espiral; Lenin señaló que concebir un desarrollo lineal, uniforme y sin retrocesos es antidialéctico, anticientífico y teóricamente falso) las condiciones para esa sociedad que dará luz, justicia y dignidad a los seres humanos, la sociedad de Rimbaud y Neruda, que hará que la poesía no haya cantado en vano.
Hasta la victoria siempre.
NOTA: La imagen de presentación del artículo ha sido tomada de: https://thenextrecession.wordpress.com/2016/10/04/the-us-rate-of-profit-1948-2015/
II.XIII. Principio Monista de Complementariedad (o modo monista complementario de descripción) (BORRADOR)
ISADORE NABI
Esta sección de la obra en construcción trata sobre los fundamentos del Marxismo en el contexto de la interpretación filosófica de la Mecánica Cuántica y de la Cosmología, específicamente sobre la interpretación dialéctica-materialista del colapso de onda y sobre el principio y fin del Universo.
III. LA DEFINICIÓN SUBJETIVA DEL VALOR COMO PRINCIPIO PSEUDOCIENTÍFICO (BORRADOR)
ISADORE NABI
Este, y otros capítulos antes subidos, pertenecen a un libro en proceso de construcción titulado “EL SISTEMA DIALÉCTICO-MATERIALISTA COMO PROGRAMA DE DEMARCACIÓN DE LAS CIENCIAS. CASO DE APLICACIÓN: LA DEFINICIÓN SUBJETIVA DEL VALOR DE LAS MERCANCÍAS COMO PRINCIPIO PSEUDOCIENTÍFICO“.
La imagen del encabezado fue tomada de http://davidharvey.org/2018/03/marxs-refusal-of-the-labour-theory-of-value-by-david-harvey/.
La valuación en la presencia de inventarios de mercancías Explorando la Interpretación Temporal y de Sistema Único de Marx
La valuación en la presencia de inventarios de mercancías
Explorando la Interpretación Temporal y de Sistema Único de Marx
Nick Potts[1]
Traducido por A. Sebastián Hdez. Solorza
Descarga el artículo completo en PDF
Resumen
Este artículo busca estimular el debate sobre cómo valuar las mercancías siguiendo la interpretación temporal y de sistema único (TSSI, por sus siglas en inglés) de la teoría del valor de Marx. Sugiero que, aun cuando Andrew Kliman y Alan Freeman siguen la TSSI de Marx, sus enfoques sobre el cálculo del valor de las mercancías son distintos. Para ilustrar esta diferencia considero un modelo simple de una economía con acervos de mercancías no vendidas que se acarrean de un periodo al otro. Concluyo que esta diferencia en el enfoque indica cuán interesante sigue siendo la investigación sobre la TSSI de Marx.
LEER EL ARTÍCULO COMPLETO AL DESCARGAR EN PDF
Notas
[1] Facultad de Negocios, Deportes…
View original post 13 more words
SOBRE LOS TENSORES: SU INTERPRETACIÓN CONCEPTUAL
Como señala (Kaplan, 1985, pág. 297), cuando se introducen coordenadas curvilíneas los métodos matriciales ya no resultan adecuados para el análisis de las operaciones vectoriales fundamentales. El análisis deseado se puede llevar a cabo con la ayuda de las estructuras matemáticas conocidas como tensores.
Los tensores son el resultado de un producto tensorial denotado como A⨂B. Un producto tensorial generaliza la noción de producto cartesiano o producto directo A × B y de suma directa A⨁B para espacios de coordenadas curvilíneas conocidos como variedades (como por ejemplo, las variedades pseudo-riemannianas bajo la cual está modelada la Teoría General de la Relatividad); lo anterior se afirma porque si se verifican las propiedades de un tensor u operador tensorial se podrá verificar que se comporta como una suma, pero su resultado (el espacio o conjunto generado) se comporta como una multiplicación. Esto está relacionado con poder generalizar nociones geométricas (que a nivel de matrices de datos tiene implicaciones en poder medir las longitudes entre los datos –y todo lo que eso implica, ni más ni menos que la base de las mediciones de todo tipo-), como por ejemplo la ortogonalidad entre vectores para una gama más general de superficies entre muchísimas otras cuestiones; de hecho, una variedad generaliza el concepto de superficie. En el lenguaje de programación R, un array multidimensional es un tensor, es decir, el resultado de un producto tensorial entre vectores, mientras que una matriz es resultado de un producto cartesiano entre vectores y es por ello que los primeros se pueden concebir geométricamente como un cubo n-dimensional o una estructura cúbica de medición con n-coordenadas, que además pueden ser curvilíneas. Una matriz es un tensor de dos dimensiones o coordenadas lineales.
Un vector es una flecha que representa una cantidad con magnitud y dirección, en donde la longitud de la flecha es proporcional a la magnitud del vector y la orientación de la flecha revela la dirección del vector.
También se puede representar con vectores otras cosas, como áreas y volúmenes. Para hacer esto, se debe hacer a la longitud del vector una magnitud proporcional a la magnitud del área a calcular y la dirección del vector debe ser ortogonal a la superficie o región de la cual se desea estimar el área o volumen.
Los vectores base o vectores unitarios (cuando la base del espacio lineal es canónica, es decir, que cada vector que conforma la base está compuesto en su pertinente coordenada por la unidad y en el resto por ceros) tienen longitud 1. Estos vectores son los vectores directores del sistema de coordenadas (porque le dan dirección a cada uno de los ejes del plano, puesto que precisamente cada uno representa un eje).
Para encontrar los componentes de un vector (en el caso de un sistema de tres coordenadas, el componente x, el componente y, el componente z) se proyecta el vector sobre el eje que corresponde al componente a encontrar, por ejemplo, si se desea encontrar el componente x del vector, la proyección se realiza sobre X. Entre mayor sea el ángulo entre un vector y un eje de referencia (X,Y,Z), menor será la magnitud del componente correspondiente a dicho eje (este componente, en este ejemplo, puede ser x, y o z); el inverso también es cierto. La magnitud de cualquier vector dentro del plano real o complejo puede determinarse como combinación lineal de los vectores base con el campo de los reales o los complejos, respectivamente. Esto implica que la magnitud de un vector (y por consiguiente de los componentes dentro del mismo, al ser una estructura lineal) puede expresarse como determinada cantidad de vectores unitarios (de longitud 1) de los diferentes ejes de coordenadas, en donde cada componente del vector se expresará unívocamente en una cantidad determinada de vectores unitarios del eje correspondiente a dicho componente.
Para generalizar los resultados anteriores a un vector de vectores A (que entre otras cosas permite agruparlos en una misma estructura matemática -por ello a nivel del programa R los arrays tienen contenido del mismo tipo y relacionado entre sí[1]-), se establece que dicho vector A tendrá los componentes A_X, A_Y, A_Z, que representan a los componentes X, Y y Z, respectivamente. Se requiere establecer un índice para cada vector (el índice es en este caso el subíndice) porque sólo existe un indicador direccional (es decir, un vector base) por componente (porque cada componente se corresponde con su respectivo eje).
Esto es lo que hace a los vectores ser tensores de rango 1, que tienen un índice o un vector base por componente. Bajo la misma lógica, los escalares pueden ser considerados tensores de rango cero, porque los escalares no tienen ningún indicador direccional (son una cantidad con magnitud, pero sin sentido) y, por consiguiente, no necesitan índice.
Los tensores son combinaciones entre componentes auxiliares de naturaleza diversa (parámetros, coeficientes, pendientes, que son en última instancia algún elemento de algún campo escalar o anillo) y componentes centrales (los miembros de la base del espacio vectorial o módulo, que expresan las variables fundamentales del sistema que se describe), que sirven para estimar de forma más robusta (en términos de precisión cuantitativa y especificidad cualitativa) las coordenadas de un sistema de referencia.
El número de índices de cada tensor será igual al número de vectores base por componente (en el caso de los tensores, los componentes y los vectores base no tienen necesariamente una relación uno-a-uno, por lo que a un componente le puede corresponder más de un vector base o vector director del sistema de coordenadas).
Considérense, por ejemplo, las fuerzas que actúan al interior de un objeto sólido cualquiera en un espacio de tres dimensiones. Este interior está segmentado en términos de superficies (que son regiones de dicho espacio a manera de planos) por los vectores base de tipo área X, Y, Z. Asúmase además que cada una de las fuerzas actúa en cada una de las regiones del espacio (esto no necesariamente es así, sólo se usa un ejemplo así para que sea más fácilmente capturable a la intuición; aunque lógico-formalmente sí es así, filosóficamente y en términos de las ciencias aplicadas no necesariamente). Lo anterior significa que, debido a la diferente dirección de los vectores base, la acción de dichas fuerzas tiene orientaciones diferentes según la región del espacio de la que se trate. Esto es así porque cada vector base tiene una dirección diferente (al menos si su dirección se estudia cuando está anclado al origen) y cada vector base determina la dirección de la acción de cada fuerza en la región del espacio que a dicho vector base le corresponde (una región -lo que de forma más general puede concebirse como una caracterización dentro de un sistema referencial- estudiada puede estar compuesta por subregiones bajo el efecto de fuerzas diferentes). Así, para poder caracterizar completamente las fuerzas que actúan dentro del objeto sólido (lo que equivale precisamente a caracterizar completamente al objeto sólido mismo -bajo las limitaciones que la teoría tiene frente a la práctica-), es necesario que cada fuerza pueda ser expresada en términos de todas las regiones del espacio en las que actúa (cada región se corresponde con un vector director o vector base), por lo que cada fuerza se debe vincular a la correspondiente cantidad regiones del sólido en las que actúa (se debe vincular a la correspondiente cantidad de vectores base a los que está asociada).
Así, los tensores permiten caracterizar completamente todas las fuerzas posibles y todas las regiones posibles sobre las que actúan tales fuerzas.
Los tensores permiten que todos los observadores en todos los sistemas de coordenadas de referencia (marco referencial, de ahora en adelante) puedan estar de acuerdo sobre las coordenadas establecidas. El acuerdo no consiste en un acuerdo sobre los vectores base (que pueden variar de un espacio a otro), tampoco en los componentes (que pueden variar según el campo escalar), sino en las combinaciones entre vectores base y componentes. La razón de lo anterior radica en que al aplicar una transformación sobre los vectores base (para pasar de un sistema referencial a otro de alguna forma equivalente), en el contexto de los tensores, la estructura algebraica resultante tendrá invariablemente una única dirección sin importar el marco referencial; por su parte, al transformar un componente se logran mantener las combinaciones entre componentes y vectores base para todos los observadores (i.e., para todos los marcos referenciales -cada observador está en un marco referencial-).
Por tanto, los tensores expresan matemáticamente (i.e., lógico-formalmente) la unidad a nivel del fenómeno (social o natural) de las fuerzas contrarias entre sí que lo componen, así como también la tensión que implica la lucha de tales fuerzas por imponerse la una a la otra durante el proceso evolutivo del fenómeno estudiado.
Como se señala en (Universidad de Granada, 2022), en el contexto de la estadística aplicada, un array es un tipo de dato estructurado que permite almacenar un conjunto de datos homogéneo, es decir, todos ellos del mismo tipo y relacionados. Cada uno de los elementos que componen un vector pueden ser de tipo simple como caracteres, entero o real, o de tipo compuesto o estructurado como son vectores, estructuras, listas.
A los datos almacenados en un array se les denomina elementos; al número de elementos de un array se les denomina tamaño o rango del vector; este rango puede determinarse de forma equivalente, en el caso de arrays multidimensionales (tensores), a través del número de ejes. Para acceder a los elementos individuales de un array se emplea un índice que será un número entero no negativo que indicará la posición del elemento dentro del array. Para referirse a una posición particular o elemento dentro del array, se especifica el nombre del array y el número de posición del elemento particular dentro del mismo, el índice.
Los arrays en gran parte se definen como las variables ordinarias, excepto en que cada array debe acompañarse de una especificación de tamaño (número de elementos). Para un array unidimensional, el tamaño se especifica con una expresión entera positiva encerrada entre paréntesis cuadrados. La expresión es normalmente una constante entera positiva.
En suma, cada dimensión de un tensor/array multidimensional (que, al ser en sí mismo una estructura de datos con las propiedades usuales de los números, es también un espacio vectorial, específicamente un espacio euclidiano) está compuesta por un número de filas y columnas especificado.
En la mayoría de los casos, los tensores se pueden considerar como matrices anidadas de valores que pueden tener cualquier número de dimensiones. Un tensor con una dimensión se puede considerar como un vector, un tensor con dos dimensiones como una matriz y un tensor con tres dimensiones se puede considerar como un paralelepípedo. El número de dimensiones que tiene un tensor se llama su rango y la longitud en cada dimensión describe su forma. El rango de un tensor es el número de índices necesarios para seleccionar de forma única cada elemento del tensor (TensorFlow, 2022). El rango también se conoce como “orden” o “grado”; como se señaló antes, otra forma de ver los tensores es como arrays multidimensionales (RStudio, 2022).
Como señala (Weisstein, 2022), formalmente hablando el rango de un tensor es el número total de índices contravariantes y covariantes de un tensor, relativos a los vectores contravariantes y covariantes, respectivamente. El rango R de un tensor es independiente del número de dimensiones N del espacio subyacente en el que el tensor se localice. Adicionalmente, se señala en la documentación R sobre el paquete ‘tensor’, que el producto tensorial de dos arrays es teóricamente un producto exterior de tales arrays colapsados en extensiones específicas al sumar a lo largo de las diagonales apropiadas. Por ejemplo, un producto matricial es el producto tensorial a lo largo de la segunda extensión de la primera matriz y la primera extensión de la segunda matriz.






En el modelo de datos multidimensional, los datos se organizan en una jerarquía que representa diferentes niveles de detalles. Un modelo multidimensional visualiza los datos en forma de cubo de datos. Un cubo de datos permite modelar y visualizar datos en múltiples dimensiones. Se define por dimensiones y hechos.
Las dimensiones son las perspectivas o entidades sobre las cuales una organización mantiene registros. Por ejemplo, una tienda puede crear un almacén de datos de ventas para mantener registros de las ventas de la tienda para la dimensión de tiempo, artículo y ubicación. Estas dimensiones permiten registro para realizar un seguimiento de las cosas, por ejemplo, las ventas mensuales de artículos y las ubicaciones en las que se vendieron los artículos. Cada dimensión tiene una tabla relacionada con ella, llamada tabla dimensional, que describe la dimensión con más detalle.
Referencias
Fleisch, D. A. (2012). What’s a tensor? Recuperado el 26 de Marzo de 2022, de Dan Fleisch: https://www.youtube.com/watch?v=f5liqUk0ZTw
geeksforgeeks. (26 de Marzo de 2022). Multidimensional Arrays in C / C++. Obtenido de geeksforgeeks.org: https://www.geeksforgeeks.org/multidimensional-arrays-c-cpp/
java T point. (Marzo de 25 de 2022). What is Multi-Dimensional Data Model? Obtenido de Data Warehouse: https://www.javatpoint.com/data-warehouse-what-is-multi-dimensional-data-model
Kaplan, W. (1985). CÁLCULO AVANZADO. MÉXICO, D.F.: COMPAÑÍA EDITORIAL CONTINENTAL, S.A. DE C.V., MÉXICO.
Patidar, P. (14 de Diciembre de 2019). Tensors — Representation of Data In Neural Networks. Obtenido de Medium: https://medium.com/mlait/tensors-representation-of-data-in-neural-networks-bbe8a711b93b
Paul, S. (12 de Septiembre de 2018). Investigating Tensors with PyTorch. Obtenido de DataCamp: https://www.datacamp.com/community/tutorials/investigating-tensors-pytorch
RStudio. (25 de Marzo de 2022). Tensors and operations. Obtenido de TensorFlow for R: https://tensorflow.rstudio.com/tutorials/advanced/customization/tensors-operations/
TensorFlow. (25 de Marzo de 2022). tf.rank. Obtenido de TensorFlow Core v2.8.0 : https://www.tensorflow.org/api_docs/python/tf/rank
Universidad de Granada. (25 de Marzo de 2022). Arrays y cadenas. Obtenido de Departamento de Ciencias de la Computación e Inteligencia Artificial de la Universidad de Granada: https://ccia.ugr.es/~jfv/ed1/c/cdrom/cap5/f_cap52.htm.
Weisstein, E. W. (25 de Marzo de 2022). Tensor Rank. Obtenido de MathWorld – A Wolfram Web Resource: https://mathworld.wolfram.com/TensorRank.html
[1] Véase (Universidad de Granada, 2022).
PROCESO DE SELECCIÓN DE VARIABLES EXPLICATIVAS EN MODELOS ESTADÍSTICOS
ISADORE NABI
# PROCESO DE SELECCIÓN DE VARIABLES EXPLICATIVAS
## Introducción: Sobre la necesidad de un proceso de selección de predictores
Usualmente se tiene interés en explicar los datos de la forma más simple, lo cual en el contexto de la teoría de las probabilidades (especialmente en la teoría bayesiana de probabilidades) se conoce como el *principio de parsimonia*, el cual está inspirado en el principio filosófico conocido como *navaja de Ockham*, la cual establece que en igualdad de condiciones la explicación más simple suele ser la más probable. El principio de parsimonia adopta diferentes formas según el área de estudio del análisis inferencial en el que se encuentre un investigador. Por ejemplo, una parametrización parsimoniosa es aquella que usa el número óptimo de parámetros para explicar el conjunto de datos de los que se dispone, pero "parsimonia" también puede referirse a modelos de regresión parsimoniosos, es decir, modelos que utilizan como criterio de optimización emplear la mínima cantidad de coeficientes de regresión para explicar una respuesta condicional Y. El principio de parsimonia, los procesos matemáticos de optimización regidos por el criterio de alcanzar un mínimo y la navaja de Ockham son un mismo tipo de lógica aplicado en escalas de la existencia (que podríamos llamar en general "materia", como lo hace Landau en sus curso de física teórica) cualitativamente diferentes. La historia de la Filosofía demuestra que el único sistema que podría ser aplicado así exitosamente es el sistema hegeliano (lo que obedece a que parcialmente sigue la lógica de la existencia misma, como han demostrado Marx, Engels, Lenin, Levins, Lewontin y el mismo Hegel en su extensa obra). ¿Cómo es posible la vinculación en distintas escalas cualitativas de la realidad del principio de la navaja de Ockham? A que todas esas ideas responden a la escuela filosófica de Ockham, que era la escuela nominalista. Retomando lo que señalan (Rosental & Iudin. Diccionario Filosófico, Editorial Tecolut, 1971. p.341; véase https://www.filosofia.org/enc/ros/nom.htm), el nominalismo fue una corriente de la filosofía medieval que consideraba (ya es una escuela extinta) que los conceptos generales tan sólo son nombres de los objetos singulares. Los nominalistas afirmaban que sólo poseen existencia real las cosas en sí, con sus cualidades individuales (es decir, las generalizaciones para ellos no tenían valor gnoseológico en sí mismas sino como recurso gnoseológico). Los nominalistas van más allá, planteando que las generalizaciones no sólo no existen con independencia de los objetos particulares (esta afirmación en correcta, lo que no es correcto es pensar que lo inverso sí es cierto), sino que ni siquiera reflejan las propiedades y cualidades de las cosas. El nominalisto se hallaba indisolublemente vinculado a las tendencias materialistas, ya que reconocía la prioridad de la cosa y el carácter secundario del concepto. Por supuesto, las generalizaciones aunque menos reales que los objetos particulares (y de ahí la sujeción de la teoría a la práctica en un concepto que las une conocido en la teoría marxista como *praxis*) no deja por ello de ser real en cuanto busca ser una representación aproximada (a largo plazo cada vez más aproximada a medida se desarrollan las fuerzas productivas) de la estructura general (interna y externa, métrica y topológica) común que tienen tales fenómenos naturales o sociales. Marx señaló que el nominalismo fue la primera expresión del materialismo de la Edad Media. Con todo, los nominalistas no comprendían que los conceptos generales reflejan cualidades reales de cosas que existen objetivamente y que las cosas singulares no pueden separarse de lo general, pues lo contienen en sí mismas (y esto no tiene un carácter únicamente marxista, sino que incluso el célebre formalista David Hilbert señaló, según la célebre biógrafa de matemáticos Constance Reid que "The art of doing mathematics consists in finding that special case which contains all the germs of generality"). Así, el defecto fundamental de la navaja de Ockham es el no considerar algún conjunto de restricciones que complementen al criterio de selección de la explicación basado en que sea la idea más simple. Como se señala en https://www.wikiwand.com/en/Occam%27s_razor,
"En química, la navaja de Occam es a menudo una heurística importante al desarrollar un modelo de mecanismo de reacción (...) Aunque es útil como heurística en el desarrollo de modelos de mecanismos de reacción, se ha demostrado que falla como criterio para seleccionar entre algunos modelos publicados seleccionados (...) En este contexto, el propio Einstein expresó cautela cuando formuló la Restricción de Einstein: "Difícilmente se puede negar que el objetivo supremo de toda teoría es hacer que los elementos básicos irreductibles sean tan simples y tan pocos como sea posible sin tener que renunciar a la representación adecuada de un dato único de experiencia"."
La clave en la expresión anterior de Einstein es "sin tener que renunciar a...", lo que se cristaliza nítidamente en una frase que señala la fuente citada es atribuida a Einstein, pero no ha sido posible su verificación: "Todo debe mantenerse lo más simple posible, pero no lo más simple". Como se verifica en https://www.statisticshowto.com/parsimonious-model/, en general, existe un *trade-off* entre la bondad de ajuste de un modelo y la parsimonia: los modelos de baja parsimonia (es decir, modelos con muchos parámetros) tienden a tener un mejor ajuste que los modelos de alta parsimonia, por lo que es necesario buscar un equilibrio.
La parsimonia estadística es deseada porque un mínimo de coeficientes de regresión implica un mínimo de variables y un mínimo de estos implica un mínimo de variables explicativas, lo que puede ser útil en casos de que exista colinealidad entre las variables explicativas, así como también permite ahorrar tiempo y dinero en lo relativo a la inversión de recursos destinada al estudio, aunque no necesariamente garantice que en general (considerando el impacto posterior de las decisiones tomadas con base en el estudio y otros factores) se ahorre tiempo y dinero.
## Modelos Jerárquicos
Existen diferentes tipos de modelos jerárquicos. Los hay de diferente tipo, algunos más complejos que otros (complejidad a nivel teórico, matemático y computacional); ejemplos de tales modelos son las mixturas de probabilidad y se pueden estudiar en https://marxistphilosophyofscience.com/wp-content/uploads/2020/12/sobre-los-estimadores-de-bayes-el-analisis-de-grupos-y-las-mixturas-gaussianas-isadore-nabi.pdf. Aquí se tratará con modelos jerárquicos más simples, como los abordados en (Kutner, Nachtsheim, Neter & Li. p.294-305).
Como señalan los autores referidos en la p.294., los modelos de regresión polinomial tienen dos tipos básicos de usos: 1. Cuando la verdadera función de respuesta curvilínea es de hecho una función polinomial. 2. Cuando la verdadera función de respuesta curvilínea es desconocida (o compleja), pero una función polinomial es una buena aproximación a la función verdadera. El segundo tipo de uso, donde la función polinomial se emplea como una aproximación cuando se desconoce la forma de la verdadera función de respuesta curvilínea, es muy común. Puede verse como un enfoque no paramétrico para obtener información sobre la forma de la función que modela la variable de respuesta. Un peligro principal en el uso de modelos de regresión polinomial es que las extrapolaciones pueden ser peligrosas con estos modelos, especialmente en aquellos con términos de orden superior, es decir, en aquellos cuyas potencias sean iguales o mayores a 2. Los modelos de regresión polinomial pueden proporcionar buenos ajustes para los datos disponibles, pero pueden girar en direcciones inesperadas cuando se extrapolan más allá del rango de los datos.
Así, como señalan los autores referidos en la p.305, el uso de modelos polinomiales no está exento de inconvenientes. Estos modelos pueden ser más costosos en grados de libertad que los modelos no-lineales alternativos o los modelos lineales con variables transformadas. Otro inconveniente potencial es que puede existir multicolinealidad grave incluso cuando las variables predictoras están centradas. Una alternativa al uso de variables centradas en la regresión polinomial es usar polinomios ortogonales. Los polinomios ortogonales están no-correlacionados, puesto que la ortogonalidad de sus términos implica independencia lineal entre los mismos. Algunos paquetes de computadora usan polinomios ortogonales en sus rutinas de regresión polinomial y presentan los resultados ajustados finales en términos tanto de los polinomios ortogonales como de los polinomios originales. Los polinomios ortogonales se discuten en textos especializados como (Drapper & Smith, Applied Linear Regression). A veces, se ajusta una función de respuesta cuadrática con el fin de establecer la linealidad de la función de respuesta cuando no se dispone de observaciones repetidas para probar directamente la linealidad de la función de respuesta.
## Caso de Aplicación
### 1. Conversión de Matriz de Datos a Marco de Datos
La base ´Vida.Rdata´ contiene datos para los 50 estados de los Estados Unidos. Estos datos son proporcionados por U.S. Bureau of the Census. Se busca establecer las relaciones que existen entre ciertas variables del Estado que se analice y la esperanza de vida. A continuación, se presenta una descripción de las variables que aparecen en la base en el orden en que
aparecen:
+ **esper**: esperanza de vida en años (1969-71).
+ **pob**: población al 1 de Julio de 1975.
+ **ingre**: ingreso per capita (1974).
+ **analf**: porcentaje de la población analfabeta (1970).
+ **crim**: tasa de criminalidad por 100000 (1976).
+ **grad**: porcentaje de graduados de secundaria (1970).
+ **temp**: número promedio de días con temperatura mínima por debajo de los 32 grados (1931-1960) en la capital del estado.
+ **area**: extensión en millas cuadradas.
Debe comenzarse leyendo el archivo de datos pertinente mediante la sintaxis `load("Vida.Rdata")`. Si se observa la estructura de la base de datos, se verifica que es simplemente una matriz. Por tanto, si se utiliza la sintaxis `names(base)` no se obtiene información alguna, mientras que si se trata de llamar a alguna de las variables por su nombre, como por ejemplo `base$esper`, R informa de un error y lo mismo ocurre si se usa `attach(base)`. Esto sucede porque la estructura de datos invocada no está definida como un marco de datos o `data.frame`. Por ello, debe comenzarse por convertir dicha matriz de datos en un marco de datos o `data.frame`y posteriormente puede verificarse si las sintaxis antes mencionadas son ahora operativas.
“`{r}
setwd(“C:/Users/User/Desktop/Carpeta de Estudio/Mis Códigos en R”)
load(“Vida.Rdata”)
names(base)
base=data.frame(base)
names(base)
“`
### 2. Obtención de todos los modelos posibles dado un determinado conjunto de variables dentro del marco de datos
Pueden obtenerse los $R^2$ ajustados de todos los modelos posibles con las 7 variables disponibles. Para hacerlo, puede construirse primero un objeto con todos los predictores y llamarlo **X** para posteriormente construir un objeto llamado **sel** aplicando la función `leaps` (perteneciente a la librería con el mismo nombre) de la siguiente forma: `sel=leaps(x,y, method="adjr2")`. Nótese que el objeto construido mediante la sintaxis `leaps`, es decir, **sel**, es una lista con 4 componentes cuyos nombres pueden obtenerse con la sintaxis `names(sel)`. Así, puede llamarse a cada uno de tales componentes por separado usando el signo `$`, por ejemplo, `sel$which`. Antes de proceder a realizar los cálculos definidos antes, se estudiará a nivel general la sintaxis `leaps`.
La sintaxis `leaps` usa un algoritmo eficiente (parsimonioso) de ramificación y cota para realizar una búsqueda exhaustiva de los mejores subconjuntos de las variables contenidas en el marco de datos para predecir y realizar análisis de regresión lineal; este tipo de algoritmo, según https://www.wikiwand.com/en/Branch_and_bound, es un paradigma de diseño de algoritmos para problemas de optimización discreta y combinatoria, así como optimización matemática. Un algoritmo de ramificación y acotación consiste en una enumeración sistemática de soluciones candidatas mediante la búsqueda en el espacio de estados: se piensa que el conjunto de soluciones candidatas forma un árbol enraizado con el conjunto completo en la raíz; "si las cosas fuesen tal y como se presentan ante nuestros ojos, la ciencia entera sobraría" dijo Marx alguna vez. El algoritmo explora las ramas del árbol representado por los subconjuntos del conjunto de soluciones posibles al problema de optimización. Antes de enumerar las soluciones candidatas de una rama, el algoritmo sigue el siguiente proceso descarte de ramas: la rama se compara con los límites estimados superior e inferior de la solución óptima y se descarta (la rama en su conjunto) si no ella puede producir una solución mejor que la mejor encontrada hasta ahora por el algoritmo (véase https://cran.r-project.org/web/packages/leaps/leaps.pdf, p.1). Como se señala en la documentación antes citada, dado que el algoritmo devuelve el mejor modelo de cada tamaño (aquí se refiere a los modelos estadísticamente más robustos según un número de variables fijo que se considere) no importa si desea utilizar algún criterio de información (como el AIC, BIC, CIC o DIC). El algoritmo depende de una estimación eficiente de los límites superior e inferior de las regiones/ramas del espacio de búsqueda. Si no hay límites disponibles, el algoritmo degenera en una búsqueda exhaustiva.
A pesar de lo señalado relativo a que la búsqueda realiza por `leaps` es independiente de cualquier criterio de información utilizado, puede omitirse este hecho con la finalidad de que sea posible incorporar a esta práctica el estudio de los criterios de información. A continuación, se presenta una lista de los mejores modelos siguiendo el criterio de $R^2$ ajustado más alto, lo que se indica al interior de la sintaxis `leaps` mediante methods="adjr2".
“`
{r}
attach(base)
library(leaps)
X=cbind(pop,ingre,analf,crim,grad,temp,area)
sel=leaps(X,esper, method=”adjr2″)
sel
names(sel)
sel$adjr2
sel$which
sel$label
sel$size
“`
Adicionalmente, es posible construir una matriz, almacenarla bajo el nombre **mat** con el contenido de las filas `sel$which` y `sel$adjr2`, agregando un contador para identificar cada modelo mediante la sintaxis `cbind`. La estructura de datos **mat** contiene todos los diferentes modelos de regresión lineal (a diferentes tamaños de los mismos) mediante la sintaxis `leaps` para la base de datos utilizada.
“`{r}
k=nrow(sel$which)
k
mat=data.frame(cbind(n=1:k,sel$which,round(sel$adjr2,2)))
mat
head(mat[order(-mat$V9),],10)
“`
Así, puede construirse un subconjunto de **mat** que contenga sólo los modelos cuyo coeficiente de determinación ajustado sea mayor o igual que 0.68.
“`{r}
subcon=subset(mat,sel$adjr2>=0.68)
head(subcon[order(-subcon$V9),],10)
“`
Nótese que los cuatro modelos con el $R^2$ ajustado más alto son los modelos 28, 38, 39, y 40, cuyo tamaño oscila entre 4 o 5 variables explicativas; si se utiliza la sintaxis `print` es posible verificar que en las filas está el modelo como tal (si la variable se toma en consideración tiene asignado un "1", mientras que en caso contrario un "0"), mientras que en las columnas se localizan las posibles variables a utilizar.
### 3. Estadístico de Mallows
Como se puede verificar en https://support.minitab.com/es-mx/minitab/18/help-and-how-to/modeling-statistics/regression/supporting-topics/goodness-of-fit-statistics/what-is-mallows-cp/, el Estadístico $C_p$ de Mallows sirve como ayuda para elegir entre múltiple modelos de regresión. Este estadístico ayuda a alcanzar un equilibrio importante con el número de predictores en el modelo. El $C_p$ de Mallows compara la precisión y el sesgo del modelo completo con modelos que incluyen un subconjunto de los predictores. Por lo general, deben buscarse modelos donde el valor del $C_p$ de Mallows sea pequeño y esté cercano al número de predictores del modelo más la constante $p$. Un valor pequeño del $C_p$ de Mallows indica que el modelo es relativamente preciso (tiene una varianza pequeña) para estimar los coeficientes de regresión verdaderos y pronosticar futuras respuestas. Un valor del $C_p$ de Mallows que esté cerca del número de predictores más la constante indica que, relativamente, el modelo no presenta sesgo en la estimación de los verdaderos coeficientes de regresión y el pronóstico de respuestas futuras. Los modelos con falta de ajuste y sesgo tienen valores de $C_p$ de Mallows más grandes que p. A continuación se presenta un ejemplo.

#Figura 1: Ejemplo del uso del Estadístico de Mallows para evaluar un modelo #Fuente: https://support.minitab.com/es-mx/minitab/18/help-and-how-to/modeling-statistics/regression/supporting-topics/goodness-of-fit-statistics/what-is-mallows-cp/
Así, para el ejemplo aquí utilizado (que responde a la base de datos antes especificada) puede obtenerse el estadístico $C_p$ de Mallows para todos los modelos posibles con las 7 variables disponibles. Para ello puede usarse la función `leaps`; nótese que no es necesario indicarle a R que obtenga el estadístico de Mallows mediante la sintaxis `method=Cp` puesto que este método es el establecido por defecto en la programación de R, por lo que en el escenario en que no se indique un "method" en específico el programa utilizará por defecto el criterio del estadístico de Mallows.
“`{r}
sel = leaps(X,esper)
names(sel)
sel$Cp
“`
Complementariamente, puede construirse una nueva matriz **mat** que en lugar de los criterios `sel$which` y `sel$adjr2` siga los criterios `sel$which`, `sel$Cp` y `sel$size`, agregando al igual que antes un contador para identificar cada modelo. Esto implicará la sobreeescritura de la matriz **mat**. Pueden seleccionarse con antelación únicamente las filas de **mat** que se corresponden con los modelos seleccionados en el punto anterior y comparar la columna del $C_p$ con la columna $size$ que corresponde al número de coeficientes (p). En cada caso puede determinarse si el modelo es sesgado o no, sin perder de vista que un modelo es sesgado según el estadístico de Mallows si $C_p>p$. De lo anterior se desprende que se está buscando un conjunto de modelos insesgados para los cuales se verifica la condición $C_p<p$ antes mencionada.
“`{r}
mat=data.frame(cbind(1:k,sel$which,round(sel$Cp,2),sel$size))
colnames(mat)[9]<-“CP”
colnames(mat)[10]<-“p”
mat[c(28,38,39,40),]
“`
Como puede observarse, en todos los modelos arrojados por la sintaxis `leaps` cumplen con la condición antes especificada, por lo que es posible afirmar que, sobre todo respecto a los modelos 28, 38, 39 y 40, que son buenos candidatos para ser utilizados (los mejores modelos son los mismos cuatro que en el literal anterior).
### 4. Suma de Cuadrados Residuales de Predicción (PRESS)
####4.1. Aproximación Gráfica
Como se señala en (https://pj.freefaculty.org/guides/stat/Regression/RegressionDiagnostics/OlsHatMatrix.pdf, p.9), la PRESS no es otra cosa que el error de estimación correspondiente a un valor particular de la variable condicional $Y$; la estimación de PRESS a veces es útil como una medida resumida de la capacidad de un modelo para predecir nuevas observaciones. Las líneas de comando presentadas a continuación expresan la configuración de la función personalizada `plot.press`, que es una función empírica que se aproxima gráficamente a los PRESS mediante el siguiente procedimiento:
a) Crea un modelo solamente con la variable **ingre**.
b) Toma el Estado i-ésimo y crea otro modelo basado en los demás Estados (excepto el i-ésimo).
c) Grafica las dos líneas de regresión y marca la observación del Estado i-ésimo en rojo para que se observe como se diferencian las dos líneas a la altura del ingreso de ese Estado.
d) Estima el promedio de la esperanza de vida para el i-ésimo Estado usando las dos ecuaciones.
“`{r}
plot.press=function(i){
mod =lm(esper~ingre,base)
mod1=lm(esper ~ ingre,base[-i,])
plot(base$ingre,base$esper,pch=18,xlab=”ingreso”,ylab=”esperanza”)
points(base$ingre[i],base$esper[i],pch=18,col=2)
abline(mod)
abline(mod1,lty=2,col=2)
abline(v=base$ingre[i],col=4,lty=2)
legend(3000,max(esper),c(“completo”,paste(“falta el “,i,sep=””)),col=c(1,2),lty=c(1,2),bty=”n”)
yi=predict(mod,data.frame(ingre=base$ingre[i]))
yii=predict(mod1,data.frame(ingre=base$ingre[i]))
res=c(yi,yii)
names(res)=c(“y_i”,”y_i(i)”)
return(round(res,2))
}
“`
Así, puede usarse la función `plot.press` con diferentes estados, por ejemplo, con Alaska (i=2) o algún otro.
“`{r}
plot.press(2)
plot.press(15)
plot.press(10)
“`
#### 4.2. Aproximación Inferencial vía Residuos Estandarizados
Como señala https://www.statisticshowto.com/what-is-a-standardized-residuals/, los residuos estandarizados permiten normalizar el conjunto de datos de estudio en el contexto del análisis de regresión y de la ejecución de pruebas de hipótesis chi-cuadrado $χ^2$. Un residuo estandarizado es una razón: la diferencia entre el valor observado y el valor esperado (condicional, a posteriori) sobre la desviación estándar del valor esperado en la prueba de chi-cuadrado.
Como se señala en https://online.stat.psu.edu/stat501/lesson/11/11.4, existen varias medidas para identificar valores extremos de X (observaciones de alto $leverage$ o $influencia$) y valores de Y inusuales (valores atípicos). Al intentar identificar valores atípicos, un problema que puede surgir es cuando existe un valor atípico potencial que influye en el modelo de regresión hasta tal punto que la función de regresión estimada se "arrastrada" hacia el valor atípico potencial, de modo que no se marca como un valor atípico utilizando el criterio usual de residuos estandarizados. Para abordar este problema, los residuos eliminados ofrecen un criterio alternativo para identificar valores atípicos. La idea básica de esto es eliminar las observaciones una a la vez, reajustando cada vez el modelo de regresión en las n – 1 observaciones restantes. Luego, se comparan los valores de respuesta observados con sus valores ajustados basados en los modelos con la i-ésima observación eliminada. Esto produce residuos eliminados (no estandarizados). La estandarización de los residuos eliminados produce residuos eliminados studentizados, como se verá teóricamente a continuación.
Formalmente, es un resultado conocido del álgebra lineal que $y=Xβ+ε$, en donde $X_{n×p}$, $\hat{β}=(X'X)^{-1}X-y$ y $\hat{y}=X\hat{β}=X(X'X)^{-1}X'y=Hy$, donde $H=X(X'X)^{-1}X'$ es la matriz conocida como *matriz sombrero*. Los residuos son $e=y-\hat{y}=y-Hy=(I-H)y$. Adicionalmente, se sabe que la varianza poblacional $σ^2$ es desconocida y puede estimarse mediante la suma de cuadrados medios del error $MSE$. Así, los residuos pueden ser expresados mediante la ecuación $e_i^*=\frac{e_i}{\sqrt{MSE}}$ y se conocen como *residuos semistudentizados*. Puesto que la varianza de los residuos depende tanto de $σ^2$ como de $X$, la varianza estimada es $\hat{V}(e_i)=MSE(1-h_{ii})$, donde $h_{ii}$ es el $i$-ésimo elemento de la diagonal principal de la matriz sombrero. Así, los residuos estandarizados, también conocidos como *residuos internamente studentizados*, tienen la forma $r_i=\frac{e_i}{\sqrt{MSE(1-h_{ii})}}$. Sin embargo, se sabe que es imposible que un residuo individual y el MSE (que es la varianza del conjunto de residuos) no estén correlacionados (existe dependencia lineal) y, por consiguiente, es imposible que $r_i$ siga una distribución t de Student. Lo anterior representa un impedimento para realizar pruebas de significancia estadística de los coeficientes de regresión, puesto que la distribución t es junto con la F los dos tipos de distribución más utilizados (y no sólo en el contexto de regresión) para realizar pruebas de hipótesis, dentro de las cuales las pruebas de significancia de coeficientes son un tipo de ellas. La solución a la problemática antes descrita consiste en eliminar la $i$-ésima observación, ajustar la función de regresión a las $n-1$ observaciones restantes y luego obtener nuevas $\hat{y}$'s que pueden ser denotadas como $\hat{y}_{i(i)}$. La diferencia $d_i=y_i-\hat{y}_{i(i)}$ es llamada *residuo eliminado*. Una expresión equivalente que no requiere recomputación es: $d_i=\frac{e_i}{1-h_{ii}}$.
Los residuos eliminados expresados de la forma anterior son la base para encontrar los residuos conocidos como *residuos eliminados studentizados* o *resiudos studentizados externamente*, los cuales adoptan la forma $t_i=\frac{d_i}{\sqrt{{\frac{MSE}{1-h_{ii}}}}}\sim{\sf t_{n-p-1}}$ o $t_i=\frac{e_i}{\sqrt{{{MSE(1-h_{ii})}}}}\sim{\sf t_{n-p-1}}$; véase https://stats.stackexchange.com/questions/99717/whats-the-difference-between-standardization-and-studentization/99723.
En lo que a la estimación de los diferentes tipos de residuos se refiere, debe comenzarse por obtener las **influencias** o **leverage** del modelo usando `hatvalues(mod)`; debe recordarse que las influencias son utilizadas para determinar que tanto impacto tiene una observación sobre los resultados de la regresión. Precisamente el análisis descriptivo anterior, en el que en una de las rectas de regresión (de las dos que aparecen en cada una de las cincuenta gráficas posibles) se omitía un Estado, tenía como finalidad verificar cuánto impactaba su ausencia (la del Estado sustraido) en la estimación realizada sobre la media condicional de $Y$. Al utilizar la sintaxis "mod=lm(esper~ingre,base)" se está planteando un modelo con la totalidad de Estados, del cual se calculan sus valores sombrero mediante la sintaxis `h = hatvalues(mod)`, sus residuos mediante `r=mod$res`, se estima el residuo de un modelo en el que no se considera el Estado i-ésimo en el análisis (en este caso Alaska) mediante `pred.r = r[2]/(1-h[2])` y, finalmente, la validez estadística de la estimación `pred.r = r[2]/(1-h[2])` se determina contrastándola con respecto al resultado de restarle a la media estimada $\hat{Y}_2$ (porque en este caso para Alaska, que ocupa la fila dos en la base de datos, que es una base de datos de corte transversal) la media estimada $\hat{Y}$ del modelo que no considera al i-ésimo Estado (aquí es Alaska).
“`{r}
mod=lm(esper~ingre,base)
h = hatvalues(mod)
r=mod$res
pred.r = r[2]/(1-h[2])
round(pred.r,2)
esper[2]-73.07
plot.press(2)
“`
Finalmente, puede obtenerse la Suma de Cuadrados Residuales de Predicción $PRESS$ utilizando los residuos eliminados globales (no únicamente para el Estado de Alaska) mediante la siguiente ecuación: $$PRESS=\sum{( \frac{r_i}{1-h_i}} )^2$$.
“`{r}
d=r/(1-h)
press=t(d)%*%d
round(press,2)
“`
### 5. Comparación de Modelos vía $PRESS$
Es posible comparar el modelo que únicamente contempla la variable ingreso **ingre** con el que se obtiene en un modelo que contenga en su lugar la cantidad de población del Estado **pop** y su tasa de criminalidad **crim**. Esto con el fin de verificar cuál de los dos modelos es más sensible a valores extremos de X al realizar estimaciones de la media condicional $\hat{Y}$ de la variable *esperanza de vida*.
“`{r}
mod=lm(esper~ingre,base)
r=mod$res
h=hatvalues(mod)
d=r/(1-h)
press=t(d)%*%d
round(press,2)
“`
“`{r}
mod2= lm(esper~pop+crim,base)
r=mod2$res
h=hatvalues(mod2)
d=r/(1-h)
press=t(d)%*%d
round(press,2)
“`
Se observa que el modelo `mod` es más sensible, puesto que su PRESS es más alto (89.32).
Debe decirse que la matriz "d" es conocida también como *matriz de Gramm*, por lo que su determinante es igual al producto de sí y su transpuesta, es decir, `t(d)%*%d`. Como se verifica en https://www.wikiwand.com/en/Gram_matrix, la matriz de Gramm cuyos elementos pertenecen a los reales tiene la característica de ser simétrica (matriz cuadrada que es igual a su transpuesta); la matriz de Gramm de cualquier base ortonormal (conjunto de vectores linealmente independientes que generan un espacio lineal -conocido como *span lineal*- denso dentro del espacio de referencia) es una matriz identidad.
El modelo anterior puede expandirse en predictores considerando ahora población **pop**, nivel de ingreso **ingre**, porcentaje de población analfebeta **analf** y la extensión en millas cuadradas **area** para explicar la esperanza de vida (medida en años).
“`{r}
mod0= lm(esper~pop+ingre+analf+area,base)
r=mod0$res
h=hatvalues(mod0)
d=r/(1-h)
press=t(d)%*%d
round(press,2)
“`
El modelo `mod0` es aún más sensible a los datos provistos por el Estado de Alaska que el modelo `mod`
Así como se amplió la cantidad de variables en consideración al pasar del modelo `mod` al modelo `mod0`, también podría realizarse el procedimiento anterior para un modelo que considere la totalidad de las variables disponibles. Una forma para evitar escribir todas las variable en es usar un punto después de **~**, además de indicar de cuál base provienen los datos. De esta forma R entiende que debe considerar todas las variables de esa base como predictores, con excepción de la variable que se indica como respuesta.
“`{r}
mod_comp= lm(esper~., base)
r=mod_comp$res
h=hatvalues(mod_comp)
d=r/(1-h)
press=t(d)%*%d
round(press,2)
“`
Como se verifica de las pruebas antes realizadas, el modelo completo `mod_comp` tiene una $PRESS$ menor (más bajo) que el modelo que utiliza 4 predictores (*i.e.*, `mod0`) para explicar la media condicional de la esperanza de vida, lo que indica menor *leverage* en relación al Estado de Alaska.
### 6. Construcción Escalonada de Modelos de Predicción
#### 6.1. Aspectos Teóricos Generales
Como se conoce de los cursos de álgebra lineal, el mecanismo de *eliminación gaussiana* o *reducción de por filas*, es un proceso secuencial de *operaciones elementales entre filas* realizadas sobre la correspondiente matriz de coeficientes con la finalidad de estimar el rango de la matriz, el determinante de una matriz cuadrada y la inversa de una matriz invertible, en cuanto este mecanismo prepara las condiciones para resolver el sistema de ecuaciones; sobre los orígenes históricos de este mecanismo debe decirse que, como se señala en https://en.wikipedia.org/wiki/Gaussian_elimination, casos particulares de este método se conocían descubiertos por matemáticos chinos (sin prueba formal) en el año 179 de la era común C.E. (que es una forma no-cristiana de expresar la era que inicia en el año en que se supone nació Jesucristo).
Los mecanismos matemáticos anteriores, utilizados en el procedimiento estadístico de selección de los predictores de la media condicional de alguna variable de respuesta, se conocen como *regresión escalonada*. Como se señala en https://en.wikipedia.org/wiki/Stepwise_regression, la regresión escalonada es un método de ajuste de modelos de regresión en el que la elección de las variables predictivas se realiza mediante un procedimiento automático (...) En cada paso, se considera una variable para sumar o restar del conjunto de variables explicativas basado en algún criterio preespecificado. Por lo general, esto toma la forma de una secuencia hacia adelante, hacia atrás o combinada de pruebas F o pruebas t. La práctica frecuente de ajustar el modelo final seleccionado seguido de reportar estimaciones e intervalos de confianza sin ajustarlos para tener en cuenta el proceso de construcción del modelo ha llevado a llamadas a dejar de usar la construcción escalonada de modelos por completo (...) o al menos asegurarse de que en el modelo la incertidumbre se refleja correctamente (...) Las alternativas incluyen otras técnicas de selección de modelos, como $R^2$ ajustado, ek criterio de información de Akaike, el criterio de información bayesiano, el $C_p$ de Mallows, la $PRESS$ o la *tasa de falso descubrimiento*.
La construcción escalonada de un modelo puede suscitarse fundamentalmente de tres maneras:
1.*Selección hacia adelante*, que implica comenzar sin variables en el modelo, comprobar lo que ocurre al adicionar cada variable utilizando un criterio de ajuste del modelo elegido, agregando la variable (si la hubiese) cuya inclusión permita la mejora estadísticamente más significativa del ajuste y repetir este proceso hasta ningún predictor mejore el modelo de manera estadísticamente significativa. Véase https://www.analyticsvidhya.com/blog/2021/04/forward-feature-selection-and-its-implementation/
2. *Eliminación hacia atrás*, que implica comenzar con todas las variables candidatas, probar la eliminación de cada variable utilizando un criterio de ajuste del modelo elegido, eliminar la variable (si la hubiese) cuya pérdida produce el deterioro más insignificante estadísticamente del ajuste del modelo, y repetir este proceso hasta que no se pueden eliminar más variables sin una pérdida de ajuste estadísticamente insignificante. Véase https://www.analyticsvidhya.com/blog/2021/04/backward-feature-elimination-and-its-implementation/?utm_source=blog&utm_medium=Forward_Feature_Elimination.
3. *Eliminación bidireccional*, una combinación de 1 y 2, probando en cada paso las variables que se incluirán o excluirán.
#### 6.2. Método de Eliminación Hacia Atrás en R
##### 6.2.1. Eliminación Hacia Atrás con Probabilidad F
Para eliminar variables secuencialmente se usa la función `drop1`, que proporciona el estadístico F correspondiente a la eliminación de una única variable explicativa; el estadístico F arrojado por esta sintaxis debe interpretarse como la probabilidad de materialización de la probabilidad de rechazar $H_0:β_1=B_2=⋯=B_i=0$ siendo esta verdadera. A causa de lo anterior, un valor F alto indica que la probabilidad de la materialización antes descrita es alta y, ante semejante riesgo, la decisión racional es fallar en rechazar $H_0$ sobre la significancia estadística nula global de los coeficientes de regresión. Fallar en rechazar $H_0$ implica que probabilísticamente hablando no existen consecuencias relevantes (a nivel de capacidad predictiva) si se elimina el modelo en cuestión, por lo que un F mayor que el nivel de significancia $α$ preestablecido (que es la probabilidad de cometer error tipo I, fijada por el investigador con base a la información histórica y a criterios de experto experimentado) significa que ese coeficiente de regresión no es estadísticamente relevante y puede eliminarse.
Puede escribirse el modelo completo (con los 7 predictores) y luego utilizar `drop1(mod,test="F")` para verificar cuál es la primera variable que se recomienda eliminar tras el proceso antes descrito. Como se adelantó, se deben eliminar aquellos predictores cuyo valor de probabilidad F sea más alto.
“`{r}
mod3=lm(esper~., base)
moda=mod3
drop1(moda,test=”F”)
“`
Si se comparan los resultados de la sintaxis `drop1` con los de `summary`, se puede verificar que las probabilidades F y t coinciden. Esto sucede en este ejemplo porque no hay variables categóricas con más de 2 categorías; sin embargo, cuando se cuenta con variables categóricas con más de 2 categorías, no se debe usar `summary` porque en tal caso las probabilidades F y t no son equivalentes.
“`{r}
summary(moda)
“`
De los resultados anteriores se desprende que el primer predictor a ser eliminado es la variable **area**, pues tiene la probabilidad F más alta. Para materializar la eliminación se puede actualizar el modelo anterior mediante `moda=update(moda,.~.-area)`.
“`{r}
moda=update(moda,.~.-area)
drop1(moda,test=”F”)
“`
Y así puede continuarse hasta que, por ejemplo, todas las probabilidades sean menores a 0.15 (o a algún valor$α$ preestablecido de la forma antes descrita).
“`{r}
moda=update(moda,.~.-analf)
drop1(moda,test=”F”)
moda=update(moda,.~.-ingre)
drop1(moda,test=”F”)
“`
Finalmente, se obtiene que el modelo sugerido contempla las variables **pop**, **crim**, **grad** y **temp**.
##### 6.2.2. Eliminación Hacia Atrás con AIC
Adicionalmente, en lugar de usar el criterio de la probabilidad F se pueden usar criterios de información. Para usar el criterio de Akaike (AIC) simplemente no se indica nada en `test`, pues el AIC es el criterio por defecto que utiliza `drop1`. En este caso, la columna de AIC indica el valor del AIC que se obtendría si se elimina esa variable. Puesto que el objetivo es aumentar el AIC (porque eso haría al predictor candidato de ser eliminado), entonces se elimina la variable que más disminuye el AIC, generando luego un nuevo modelo (con las variables que menos disminuyen el AIC) que se compara con el modelo anterior, y así sucesivamente, hasta que la eliminación de cualquier variable aumenta el AIC con respecto al modelo anterior en lugar de disminuirlo, puesto que esta es la señal que en términos de robustez estadística del modelo no es recomendable eliminar más predictores.
“`{r}
moda=mod3
drop1(moda)
moda=update(moda,.~.-area)
drop1(moda)
moda=update(moda,.~.-analf)
drop1(moda)
moda=update(moda,.~.-ingre)
drop1(moda)
“`
El procedimiento antes descrito se puede realizar de forma automática con la sintaxis `step` mediante`step(mod)`. Tras ello, puede almacenarse el resultado en una estructura de datos (aquí llamada "mod4"#") y aplicar `summary` sobre dicho objeto.
“`{r}
mod4=step(mod3)
summary(mod4)
“`
##### 6.2.2. Eliminación Hacia Atrás con BIC
###### 6.2.2.1. Aspectos Teóricos Relevantes del BIC
Si en lugar del criterio AIC se desease utilizar el criterio bayesiano de información (BIC) se debe indicar en la sintaxis `step` mediante `k=log(n)`. Debe agregarse que, como se señala en (Bishop, Christopher M. Pattern Recognition and Machine Learning. 2006, p. 217), el criterio bayesiano de información penaliza la complejidad del modelo y es el criterio expuesto por Bishop en el lugar referido el que muestra la penalización que el BIC ejerce sobre la complejidad del modelo y que se conoce como *factor de Occam*.
“`{r}
knitr::include_graphics(“FOTO4.JPG”)
“`

#Figura 2: Evaluación de la log-verosimilitud empleando parámetros optimizados #Fuente: Bishop, Christopher M. Pattern Recognition and Machine Learning. 2006, p. 216-17.
Debe decirse sobre el factor de Occam que, como puede verificarse en [David J. Spiegelhalter, Nicola G. Best, Bradley P. Carlin & Angelika Van Der Linde. Bayesian measures of model complexity and fit. Journal of Royal Statistical Society, Series B (Statistical Methodology); https://rss.onlinelibrary.wiley.com/doi/pdf/10.1111/1467-9868.00353] y en (van der Linde, Angelika. A Bayesian view of model complexity. Statistica Neerlandica xx, year xx-xx, special issue: All Models Are Wrong...; https://statmodeling.stat.columbia.edu/wp-content/uploads/2013/08/snavdlmc.pdf), no existe una definición analítica para el mismo, *i.e.*, una definición que pueda ser sustentada lógicamente desde algún marco teórico en congruencia clara y directa con un marco matemático autodemostrable dentro de teoría de conjuntos ZF-C (Zermelo-Fraenkel con Axioma de Elección) que la modele.
En este sentido, la investigación de Spiegelhalter et al es una de las investigaciones más importantes de al menos las últimas dos décadas a nivel de la teoría de las probabilidades y su importancia es aún mayor si el marco de referencia es únicamente la teoría bayesiana de probabilidades. En síntesis, los autores y autora de la investigación concluyen que la medida de complejidad bayesiana (que es la estructura matemática que aparece en la obra citada de Christopher Bishop) tiene como trasfondo común con el criterio DIC (que es la versión generalizada del AIC, de naturaleza teórica frecuentista, que tiene su propia penalización de la complejidad del modelo y por consiguiente su propia medición de dicha complejidad) la teoría de la información (rama de la teoría de las probabilidades que versa sobre las estructuras matemáticas que rigen la transmisión y el procesamiento de la información y se ocupa de la medición de la información y de la representación de la misma, así como también de la capacidad de los sistemas de comunicación para transmitir y procesar información; véase https://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_informaci%C3%B3n), que el DIC y el BIC tienen una justificación lógica similar aunque el DIC tiene una campo de aplicación más amplio. Adicionalmente, se señala que la metodología de medición de complejidad bayesiana que ellos proponen es aplicable a toda la clase de modelos y que únicamente requiere de un trabajo analítico "despreciable" (p. 613) relativo a la configuración de un muestreo del tipo Monte Carlo basado en cadenas de Markov. Además, existe un problema señalado por los autores y autora relativo a que es difícil explicar si las diferencias entre los criterios de medición de complejidad del BIC y del DIC son realmente diferentes en términos estadísticos, puesto que es aún más difícil determinar el error del DIC en pruebas Monte Carlo (para ello se cita una investigación previa que señala esta dificultad). La publicación de este documento de investigación generó la apertura de un debate alrededor del mismo, que contó con la participación de S. Brooks (University of Cambridge), Jim Smith (University of Warwick), Aki Vehtari (Helsinki University of Technology), Martyn Plummer (International Agency of Research on Cancer, Lyon), Mervyn Stone (University College London), Christian P. Robert (Université Paris Dauphine) y D. M. Titterington (University of Glasgow), el mismísimo J. A. Nelder en persona (Impercial College of Science, Techonology and Medicine, London), Anthony Atkinson (London School of Economics and Political Science), A. P. David (University College London), José M. Bernardo (Universitat de València), Sujit K. Sahu (University of Southampton), Sylvia Richardson (Imperial College School of Medicine, London), Peter Green (University of Bristol), Kenneth P. Burnham (US Geological Survey and Colorado State University, Fort Collins), María Delorio (University of Oxford) y Christian P. Robert (Université Paris Dauphine), David Draper (University of California, Santa Cruz), Alan E. Gelfand (Duke University Durkham) y Matilde Travisani (University of Trieste), Jim Hodges (University of Minesota, Minneapolis), Youngjo Lee (Seoul National University), Xavier de Luna (Uméa University) y, finalmente, Xiao-Li Meng (Harvard University, University of Chicago); tremendo crossover, mucho mejor que *Crisis en Tierras Infinitas (1985-86)*... palabras mayores. Los posicionamientos de los autores y autoras participantes son diversas y profundas, sin embargo, se hará una recapitulación de aquellos que señalen debilidades la medición bayesiana de complejidad de un modelo estadístico.
Brooks (p. 616-18) plantea que la investigación (como casi toda buena investigación) deja preguntas abiertas, específicamente él señala que la ecuación 9 de la página 587 utiliza para calcular dicha complejidad el valor esperado, pero ¿por qué no la moda o la mediana?, ¿cuál es la justificación teórica de ello?, y de ello se deriva también ¿cómo se debe decidir entonces que el parámetro estimado debe ser la media, la moda o la mediana?, lo cual es relevante en cuanto podría conducir a diferencias importantes con el DIC; finalmente, ¿cómo se pueden ser comparables el análisis del modelo bajo el DIC con el análisis del modelo bajo las probabilidades posteriores (enfoque bayesiano) y por qué difieren?, ¿pueden ambas ser "correctas" de alguna manera significativa?
Por su parte, Jim Smith (p. 619-20) señala que no encontró errores técnicos (*i.e.*, matemáticos), pero que encontró cuatro problemas fundacionales. El primero que señala es que las implicaciones predictivas de todas las configuraciones del prior relativas a las variaciones en los ejemplos resueltos en la Sección 8 son increíbles (no en un sentido que podría considerarse positivo), puesto que según Smith no representan juicios de expertos cuidadosamente obtenidos, sino las opiniones de un usuario de software vacío. También señala que, al principio de la Sección 1, los autores afirman que quieren identificar modelos sucintos que parecen describir la información [¿acerca de valores de parámetros "verdaderos" incorrectos (ver Sección 2.2)?] en los datos con precisión, sin embargo, señala también que en un análisis bayesiano, la separación entre la información de los datos y el prior es artificial e inapropiada; señala que "Un análisis bayesiano en nombre de un experto en auditoría remota (Smith, 1996) podría requerir la selección de un prior que sea robusto dentro de una clase de creencias de diferentes expertos (por ejemplo, Pericchi y Walley (1991)). A veces, los prior predeterminados pueden justificarse para modelos simples. Incluso entonces, los modelos dentro de una clase de selección deben tener parametrizaciones compatibles: ver Moreno et al. (1998). Sin embargo, en los ejemplos en los que "el número de parámetros supera en número a las observaciones", afirman que sus enfoques de enfoque, es poco probable los prior predeterminados (por defecto) muestren alguna robustez (estadística). En particular, fuera del dominio de la estimación local vaga o de la estimación de la varianza de separación (discutida en la Sección 4), aparentemente los antecedentes por defecto pueden tener una fuerte influencia en las implicaciones del modelo y, por lo tanto, en la selección.", de lo cual se deriva una razonable insatisfacción ante la expresión la afirmación de los autores y autora sobre la baja probabilidad de que los prior muestren robustez.
Martyn Plummer (p. 621) señala lo que a su juicio son debilidades en la derivación heurística del DIC y de ello se deriva su señalamiento de sustento formal ;como señalan (Rosental & Iudin. Diccionario Filosófico. Editorial Tecolut, 1971. p. 215-216),
en términos históricos la palabra "heurística" proviene del griego εὑρίσκω, que significa "discuto". Es el arte de sostener una discusión y floreció sobre todo entre los sofistas de la antigua Grecia. Surgida como medio de buscar la verdad a través de la polémica, se escindió pronto en dialéctica y sofística. Sócrates, con su método, desarrolló la primera. En cambio, la sofística, tendiente sólo a alcanzar la victoria sobre el contrincante en la discusión, redujo la heurística a una suma de procedimientos que podían aplicarse con el mismo éxito tanto para demostrar una aseveración, cualquiera que fuese, como para refutarla. De ahí que ya Aristóteles no estableciera ninguna diferencia entre heurística y sofística. En la actualidad, al hablar de métodos heurísticos se hace referencia a una especie de atajos para las derivaciones rigurosas que implican mayor costo computacional, por lo que su carácter de verdad es siempre de corto plazo (provisional).
Mervyn Stone (p. 621) señala que la investigación de 2002 "bastante económico" en lo relativo a la *verdad fundamental* (véase https://marxistphilosophyofscience.com/wp-content/uploads/2020/12/sobre-los-estimadores-de-bayes-el-analisis-de-grupos-y-las-mixturas-gaussianas-isadore-nabi.pdf, p. 43-44), que si la sección 7.3 pudiera desarrollarse rigurosamente (puesto que le parece gnoseológicamente cuestionable el uso de $E_Y$), "(...) otra conexión (a través de la ecuación $(33)$) podría ser que $DIC ≈ −2A$. Pero, dado que la sección 7.3 invoca el supuesto de "buen modelo" y pequeños $|\hat{θ}-θ|$ para la expansión de la serie de Taylor (es decir, $n$ grande), tal conexión sería tan artificial como la de $A$ con el criterio de información de Akaike: ¿por qué no seguir con la forma prístina (hoy en día calculable) de $A$, que no necesita $n$ grande o verdad? , ¿y cuál acomoda la estimación de θ en el nivel de independencia de un modelo bayesiano jerárquico? Si la sensibilidad del logaritmo a probabilidades insignificantes es objetable, los bayesianos deberían estar felices de sustituirlo por una medida subjetivamente preferible de éxito predictivo." Es imposible cuestionar a Stone en cuanto a que, dado el enseñoramiento que en la teoría bayesiana de probabilidades tiene la escuela bayesiana subjetiva, el promedio del gremio bayesiano estaría filosóficamente satisfecha con renunciar a elementos objetivos (en este caso son requerimientos preestablecidos por la teoría del aprendizaje estadístico que condicionan la validez gnoseológica del modelo propuesto como un todo, como una muestra grande y/o una verdad fundamental) si representan un punto de discordia y pueden ser sustituidos por algún criterio de decisión que pueda ser determinado; que en paz descanse su alma https://www.ucl.ac.uk/statistics/sites/statistics/files/meryvn-stone-obituary.pdf.
Christian P. Robert y D. M. Titterington (p. 621) señalan que la estructura matemática planteada por los autores de la investigación para determinar la complejidad de un modelo desde la perspectiva bayesiana parecería hacer un uso duplicado (repetido en dos ocasiones) del conjunto de datos, la primera vez lo hacen para determinar la distribución posterior y la segunda para calcular la verosimilitud observada (o verosimilitud a priori, sin considerar información adicional). Este uso duplicado del conjunto de datos puede conducir a un sobreajuste del modelo; señalan que este tipo específico de problemática surgió antes en la investigación de (Aitkin, 1991).
Seguramente el invitado más célebre entre todos los que asistieron a este maravilloso coloquio académico fue John Nelder, padre de los modelos lineales generalizados. Antes de exponer su planteamiento, deben introducirse algunas cuestiones. En primer lugar, el *escape de amoníaco* en aplicaciones industriales es a lo que los autores se refieren (y se refirará Nelder) como *stack loss* (p. 609). En segundo lugar, la tabla 2 a la que se referirá Nelder es la siguiente:
“`{r}
knitr::include_graphics(“TABLA2.JPG”)
“`

#Figura 3: Tabla 2. Resultados de desviación para los datos de pérdida de amoníaco. #Fuente: Spiegelhalter, Best, Carlin & van der Linde. Bayesian measures of model complexity and fit, p. 610.
Así, Nelder (p. 622) señala: "Mi colega, el profesor Lee, ha planteado algunos puntos generales que conectan el tema de este artículo con nuestro trabajo sobre modelos lineales generalizados jerárquicos basados en la probabilidad. Quiero plantear un punto específico y dos generales. (a) El profesor Dodge ha demostrado que, de las 21 observaciones en el conjunto de datos de pérdida de amoníaco, ¡solo cinco no han sido declaradas como valores atípicos por alguien! Sin embargo, existe un modelo simple en el que ninguna observación aparece como un valor atípico. Es un modelo lineal generalizado con distribución gamma, log-link y predictor lineal x2 + log.x1 / Å log.x3 /: Esto da las siguientes entradas para la Tabla 2 en el documento: 98.3 92.6 6.2 104.5 (estoy en deuda con el Dr. Best por calcularlos). Es claramente mejor que los modelos existentes usados en la Tabla 2. (b) Este ejemplo ilustra mi primer punto general. Creo que ha pasado el tiempo en que bastaba con asumir un vínculo de identidad para los modelos y permitir que la distribución solo cambiara. Deberíamos tomar como nuestro conjunto de modelos de línea base al menos la clase de modeloos lineales generalizados definida por distribución, enlace y predictor lineal, con la elección de escalas para las covariables en el caso del predictor lineal. (c) Mi segundo punto general es que, para mí, no hay suficiente verificación de modelos en el artículo (supongo que el uso de tales técnicas no va en contra de las reglas bayesianas). Por ejemplo, si un conjunto de efectos aleatorios es suficientemente grande en número y el modelo postula que están distribuidos normalmente, sus estimaciones deben graficarse para ver si se parecen a una muestra de tal
distribución. Si parecen, por ejemplo, fuertemente bimodales, entonces el modelo debe revisarse." Que en paz descanse su alma.
Anthony Atkinson (p. 622) señala que dirige su participación al contexto de la regresión, concluyendo que este criterio de selección de modelos (el BIC planteado por los autores, que es el estimado mediante la sintaxis de R) es un primer paso, que necesita ser complementado
mediante pruebas de diagnóstico y gráficos. Para finalizar plantea que "Estos ejemplos muestran que la búsqueda hacia adelante es una herramienta extremadamente poderosa para este propósito. También requiere muchos ajustes del modelo a subconjuntos de datos. ¿Puede combinarse con los apreciables cálculos de los métodos de Monte Carlo de la cadena de Markov de los autores?" Que en paz descanse su alma.
A.P. Dawid plantea que el artículo debería haberse titulado "Medidas de la complejidad y el ajuste del modelo bayesiano", ya que según él son los modelos, no las medidas, los que son bayesianos. Una vez que se han especificado los ingredientes de un problema, cualquier pregunta relevante tiene una respuesta bayesiana única. La metodología bayesiana debe centrarse en cuestiones de especificación o en formas de calcular o aproximar la respuesta. No se requiere nada más (...) Un lugar donde un bayesiano podría querer una medida de la complejidad del modelo es como un sustituto de p en la aproximación del criterio de información de Bayes a la probabilidad marginal, por ejemplo, para modelos jerárquicos. Pero en tales casos, la definición del tamaño de muestra $n$ puede ser tan problemática como la de la dimensión del modelo $p$. Lo que necesitamos es un mejor sustituto del término completo $p⋅log(n)$". En línea con la gnoseología marxiana, lo adecuado parecería ser considerar que tanto los modelos como las medidas son bayesianos (o de otra escuela de filosofía de las probabilidades).
Las participaciones restantes son no tanto relativas a cuestiones metodológicas como a cuestiones filosóficas-fundacionales de la teoría bayesiana de las probabilidades y de la teoría de las probabilidades en general (puesto que el DIC, que es un criterio de información presentado por los mismos autores que presentan el BIC, no es bayesiano debido a que es una generalización del AIC -que es frecuentista-); de hecho, la transición de cuestiones metodológicas a filosóficas-fundacionales se expresa en el planteamiento de Dawid, quien aunque aborda cuestiones metodológicas lo hace con base en la lógica filosófica de que los modelos y no las medidas son los que pueden ser (o no) bayesianos. Por supuesto, estas últimas son las participaciones más importantes, sin embargo, abordalas escapa a los límites de esta investigación, por lo que para tan importante tarea se dedicará indudablemente un trabajo posterior.
###### 6.2.2.2. Ejecución de la Eliminación Hacia Atrás con el BIC
“`{r}
n = nrow(base)
mod5=step(mod3,k=log(n))
summary(mod5)
“`
#### 6.3. Método de Selección Hacia Adelante en R
A propósito de lo señalado por Anthony Atkinson, para realizar un proceso de selección hacia adelante se puede usar la función `add1` inciando con un modelo que no contenga ninguna variable e indicando en `scope` cuales son todas las variables disponibles. Ello se realiza de la siguiente forma: `add1(modb, scope=~pop + ingre + analf + crim + grad + temp + area)`.
“`{r}
mod6 = lm(esper~1,base)
modb=mod6
add1(modb, scope=~pop + ingre + analf + crim + grad + temp + area)
“`
En este caso se escoge agregar la variable que disminuya más el AIC. En este caso es **crim**. Se actualiza el modelo y se continúa hasta que todas tengan un AIC más bajo que el anterior: `modb=update(modb,.~.+crim)`.
“`{r}
modb=update(modb,.~.+crim)
add1(modb, scope=~pop + ingre + analf + crim + grad + temp + area)
modb=update(modb,.~.+grad)
add1(modb, scope=~pop + ingre + analf + crim + grad + temp + area)
modb=update(modb,.~.+temp)
add1(modb, scope=~pop + ingre + analf + crim + grad + temp + area)
modb=update(modb,.~.+pop)
add1(modb, scope=~pop + ingre + analf + crim + grad + temp + area)
“`
De forma similar se puede usar `step` para indicar `scope` (además de indicar `direction="forward"`) de la siguiente forma: `step(mod6,direction="forward",scope=~pop + ingre + analf + crim + grad + temp + area)`. `scope` "define la gama de modelos examinados en la búsqueda por pasos. Debe ser una fórmula única o una lista que contenga los componentes superior e inferior, ambas fórmulas. Consulte los detalles sobre cómo especificar las fórmulas y cómo se utilizan." (véase https://stat.ethz.ch/R-manual/R-devel/library/MASS/html/stepAIC.html).
En este caso, tiene la logica del modelo hacia adelante, se va ingresando las variables que reducen el AIC y luego quedan las que no estan en el modelo, osea las que incrementaria el AIC.
“`{r}
mod7=step(mod6,direction=”forward”,scope=~pop + ingre + analf + crim + grad + temp + area)
summary(mod7)
“`
The three contradictions of the Long Depression
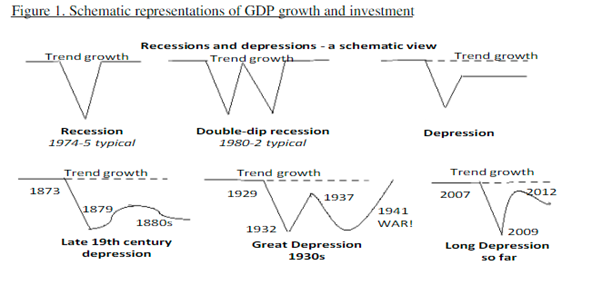
One of my basic theses about modern capitalism is that since 2008, the major capitalist economies have been in what I call a Long Depression. In my book of 2016 of the same name, I distinguish between what economists call recessions or slumps in production, investment and employment; and depressions. Under the capitalist mode of […]
The three contradictions of the Long Depression
SOBRE LA VISIÓN MARXISTA DE LA EXISTENCIA COMO ESTRUCTURA ORGÁNICA OBJETIVA (BORRADOR)
II.XI. Ley de Conexión Universal y Acción Recíproca
Como señalan (Fundación Gustavo Bueno, 2021), (Rosental & Iudin, 1971, págs. 78-79) y (Frolov, 1984, págs. 76-77), la conexión y la acción recíproca entre los objetos y los fenómenos de la Naturaleza y de la Sociedad tienen un carácter universal. La dialéctica materialista sostiene por eso, que ni un solo fenómeno de la Naturaleza y de la Sociedad puede ser comprendido si se le toma fuera de sus conexiones con los fenómenos circundantes. Por ejemplo, el sistema solar representa un todo único, todas sus partes se hallan en conexión mutua, en acción recíproca. La conexión mutua tiene lugar entre los animales y las condiciones geográficas que los rodean. En la sociedad humana, todas sus parten se hallan también en la más íntima relación mutua y recíproco condicionamiento. Así, tal o cual ideología puede ser comprendida sólo en relación con todo el conjunto de las condiciones materiales de la vida de la sociedad, con la lucha de clases, etc. Todo régimen y movimiento sociales que aparecen en la historia deben ser juzgados desde el punto de vista de las condiciones que los han engendrado y a los que se hallan vinculados; el régimen de la esclavitud, dentro de las condiciones modernas, es un absurdo, pero dentro de las condiciones de desintegración del régimen del comunismo primitivo era un fenómeno perfectamente lógico y natural, y representaba un progreso en comparación con el comunismo primitivo. De igual forma, no se puede explicar científicamente un fenómeno tal como las guerras imperialistas si se las separa del modo de producción capitalista, de las contradicciones efectivas del capitalismo. Por eso hay que abordar cada fenómeno desde el punto de vista histórico. Lo que es real y natural en unas condiciones históricas pierde todo sentido en otras. La existencia de la acción recíproca entre los fenómenos no supone que todas las causas y efectos sean importantes en igual grado: el método dialéctico exige que se indaguen las bases de esa interacción, que se establezcan las causas decisivas, fundamentales, que condicionaron tal o cual fenómeno.
Así, por oposición a la metafísica, la dialéctica materialista no considera la naturaleza como un conglomerado casual de objetos y fenómenos, desligados y aislados unos de los otros y sin ninguna relación de dependencia entre sí (puesto que ello termina siempre por derivar en una concepción de la naturaleza como una aglomeración caótica de hechos accidentales), sino como un todo articulado y único, en el que los objetos y fenómenos se hallan orgánicamente vinculados unos a otros, dependen unos de otros y se condicionan los unos a los otros. Por eso, el método dialéctico entiende que ningún fenómeno de la naturaleza puede ser comprendido si se le enfoca aisladamente, sin conexión con los fenómenos que le rodean, pues todo fenómeno, tomado de cualquier campo de la naturaleza, puede convertirse en un absurdo, si se le examina sin conexión con las condiciones que le rodean, desligado de ellas; y por el contrario, todo fenómeno puede ser comprendido y explicado, si se le examina en su conexión indisoluble con los fenómenos circundantes y condicionado por ellos.
Sin embargo, la dialéctica materialista plantea que no basta tener en cuenta el encadenamiento de causas y efectos, sino que es preciso subrayar también que la causa y el efecto actúan el uno sobre el otro. Así, todo régimen político está determinado por el régimen económico que lo ha engendrado. Pero a su vez, el poder político ejerce una influencia considerable sobre el régimen económico. No es posible analizar el modo de producción capitalista, que se halla desgarrado por las contradicciones y no es más que una traba al desarrollo de las fuerzas productivas, sin tener en cuenta el papel que desempeña el poder político de la burguesía, pues ésta, todavía en el poder, trata de eternizar por todos los medios el modo de producción fundado sobre la explotación del hombre por el hombre. Los fenómenos deben ser enfocados desde el punto de vista de su interacción y de su condicionamiento recíproco, pues se cometería un error grosero si sólo se dijera que las relaciones de producción están en función de las fuerzas productivas. Sería un procedimiento unilateral, porque, engendradas por las fuerzas productivas, las relaciones de producción desempeñan, si corresponden a las fuerzas productivas, un papel importantísimo en el desarrollo de estas últimas (y en caso contrario, un papel importantísimo en el freno a su desarrollo).
El alcance y la importancia del principio de la conexión y de la interacción de los fenómenos, reside en que destaca claramente un hecho esencial: el mundo real está regido por leyes. El encadenamiento de los fenómenos significa que las contingencias no dominan en la naturaleza y en la sociedad; que son las leyes objetivas, independientes de la voluntad y de la conciencia humanas, las que determinan el desarrollo. La conexión y la interacción de la causa y del efecto condicionan el curso necesario de los fenómenos de la naturaleza y la vida social. Hay que estudiar los regímenes y los movimientos sociales desde el punto de vista de las condiciones que los han engendrado y a las cuales están vinculados. En nuestros días, sería absurdo el régimen de esclavitud, mientras que en la época en que la comuna primitiva se disgregaba, representaba un fenómeno necesario, un paso adelante. Del mismo modo, el régimen capitalista, progresivo en ciertas condiciones históricas, constituye hoy un obstáculo al progreso de la sociedad.
Saber abordar los hechos reales es tener en cuenta las condiciones concretas de lugar y tiempo, por lo que la concatenación de los fenómenos de la forma antes expuesta ayuda a mostrar la sofística y el eclecticismo que reside en aquellas separaciones arbitrarias de ciertos aspectos de un fenómeno complejo, en la confusión de considerar equivalentes condiciones históricas diferentes, en la transposición mecánica en una situación nueva lo que no es valedero sino en una situación dada, etc.
Esta ley es la ley más general de la existencia del mundo; constituye el resultado y la manifestación de la interacción universal de todos los objetos y fenómenos, es la regularidad más general de la existencia del mundo. Expresa la unidad estructural interna de todos los elementos y propiedades en cada sistema íntegro, así como los nexos y relaciones infinitamente diversos del sistema dado con los sistemas o fenómenos que le rodean. En esta ley se manifiestan la unidad del mundo material y la determinación de cualquier fenómeno por otros procesos materiales, es decir, la interacción universal de los cuerpos condiciona la existencia misma de los objetos materiales concretos y todas sus peculiaridades específicas. La conexión universal de los fenómenos tiene manifestaciones infinitamente diversas. Incluye las relaciones entre las propiedades particulares de los cuerpos o de los fenómenos concretos de la naturaleza, relaciones que encuentran su expresión en leyes específicas; también incluye las relaciones entre las propiedades universales de la materia y las tendencias de desarrollo que encuentran su manifestación en las leyes dialécticas universales del ser. De ahí que toda ley sea una expresión concreta de la conexión universal de los fenómenos. Gracias a tal conexión, el mundo no constituye un amontonamiento caótico de fenómenos, sino un proceso universal único, sujeto a ley del movimiento, es decir, es un proceso lógico único de movimiento y desarrollo de la materia.
Los nexos entre los objetos y los fenómenos pueden ser directos o indirectos, permanentes o temporales, esenciales o inesenciales, casuales o necesarios, funcionales (dependencia funcional) o no funcionales, etc. La conexión universal de los fenómenos se halla estrechamente vinculada a la causalidad, más la causa y el efecto como tales sólo pueden ser examinados al margen de la conexión universal de unos fenómenos con otros. Si la causa y el efecto, por el contrario, se ponen en conexión con el todo, pasan una al otro, se transforman en conexión e interacción universales. Constituye un caso particular de esta interconexión la retroconexión en todos los sistemas que se regulan automáticamente.
Debe establecerse además que no es posible reducir a la mera interacción física de los cuerpos el nexo entre los fenómenos, puesto que, aparte de ella, existen relaciones biológicas y sociales incomparablemente más complejas que se subordinan a sus leyes específicas. A medida que avanza el desarrollo de la materia y va pasando a formas más elevadas de organización, se complican también las formas de interconexión de los cuerpos, aparecen especies de movimiento cualitativamente nuevas. Esta ley impera asimismo en lo que respecta al desenvolvimiento de la sociedad humana, en la cual, a medida que progresan los modos de producción y la civilización se desarrolla, se hacen más complejos los nexos entre los individuos y los estados, se diversifican cada vez más las relaciones políticas, económicas, ideológicas, etc. Este concepto es de gran alcance cognoscitivo. El mundo objetivo sólo puede conocerse investigando las formas de conexión causales y de otro tipo entre los fenómenos, delimitando los nexos y relaciones más esenciales, etc., es decir, a través de la investigación multilateral y sistemática de cualesquiera objetos y la segregación de todas las conexiones y relaciones esenciales, así como de las leyes de tales conexiones. El progreso del conocimiento cobra realidad en el movimiento del pensar, que pasa de reflejar conexiones menos profundas y generales a establecer nexos y relaciones más profundos y más generales entre los fenómenos y procesos. La estructura misma de las ciencias y su clasificación constituyen un reflejo de la conexión universal de los fenómenos. Así se explica que con el progreso del saber científico los lazos y la interacción de las ciencias entre sí se hagan cada vez más estrechos, y que surjan ciencias “limítrofes” que anudan esferas del saber antes separadas (por ejemplo, la bioquímica, la astrofísica, etc.).
Como una demostración parcial de esta ley, la más general entre las leyes de la dialéctica y de la existencia de la realidad misma, se estudiará la investigación de (Vitiello, 2014), que muestra que existe un isomorfismo entre sistemas disipativos, sistemas fractales auto-similares y sistemas electrodinámicos, lo que plantea, en según sus palabras, una “visión integrada de la Naturaleza” (p. 203).
Como señala (Lesne, Renormalization Methods, 1998, pág. 1), en aproximadamente los últimos cincuenta años han aparecido en la comunidad científica, primero en la teoría de campos y luego en varios otros dominios como la física estadística y los sistemas dinámicos, los términos “métodos de renormalización”, “grupo de renormalización” y “operadores de renormalización”. Las técnicas analíticas a las que se refieren estas expresiones son fundamentales para el estudio de lo que se conoce como fenómenos críticos, por el fracaso de los métodos anteriores; su desarrollo siguió a la aparición de la noción de invariancia de escala.” Así, ejemplos concretos, como la transición líquido-gas de una sustancia pura, sugieren la distinción entre los siguientes tipos de sistemas:
- Sistemas homogéneos a gran escala, ilustrado por la imagen de un tablero de ajedrez.
- Sistemas críticos auto-similares, ilustrados por la imagen de un globo, y cuyas propiedades macroscópicas se expresan mediante leyes de escala; los métodos de renormalización son esenciales aquí. Fueron concebidos para dar un valor explícito a los exponentes asociados y mostrar sus propiedades de universalidad, si las hubiese.
Figura 2: Fenómeno Crítico como Superposición Estable de Fase Sólida y Fase Líquida

Un fenómeno crítico es aquel que ocurre cuando, como resultado de la acción de fuerzas (para el ejemplo gráfico dado, estas fuerzas imprimen presión y temperatura sobre el sistema físico del entorno sobre un determinado sistema en una magnitud que excede el umbral[1]), dicho sistema manifiesta una coexistencia estable entre dos fases (estados), cuando regularmente estos estados están ligados entre sí en algún orden temporal (i.e., no-simultáneo).
Como señala (Lesne, Renormalization Methods, 1998, pág. 2), las nociones sobre el comportamiento colectivo de los grados de libertad en sistemas estadísticos que analizan el mundo microscópico es revelada por el estudio de las fluctuaciones y de las correlaciones estadísticas, mientras que la noción de fenómeno crítico[2], que es precisamente resultante del comportamiento colectivo antes descrito, es una noción perceptible en todas las escalas y versa sobre la divergencia crítica (respecto de un valor crítico) de ciertas cantidades macroscópicas descritas por las leyes de escala y por sus exponentes (conocidos como exponentes críticos).
Comprendido lo anterior, puede exponerse sobre terreno firme el concepto de auto-similaridad. Este concepto, también conocido como invarianza escalar para el caso continuo, significa que “(…) Nada importante se modifica en la física del estado crítico si cambiamos la escala de observación (…) Por ejemplo, a medida que disminuimos el aumento de un microscopio imaginario, tan pronto como ya no vemos los detalles microscópicos, la imagen del sistema físico permanece estadísticamente igual. Esta propiedad de invarianza escalar del estado crítico fue destacada y utilizada en la década de 1960 por Kadanoff, quien tuvo la intuición de que esta sería la clave para una descripción eficaz de los fenómenos críticos. De hecho, en 1970 varios físicos, en particular Wilson, propusieron una serie de métodos denominados “grupo de renormalización” que permitían el cálculo de comportamientos críticos extrayendo las consecuencias físicas de la invarianza de escala (…) Una de estas consecuencias es que los comportamientos críticos no dependen en gran medida en detalles físicos microscópicos que se “promedian” a gran escala. Sin embargo, dependen en gran medida de las características geométricas del sistema: la dimensión espacial y el número n de componentes del parámetro de orden.” (Lesne & Laguës, Scale Invariance. From Phase Transitions to Turbulence, 2012, págs. 30-31). Como señala, (Lesne, Renormalization Methods, 1998, pág. 2), las nociones de invariancia de escala y auto-similaridad, a través de la ruptura de la simetría, reemplazan la noción de homogeneidad y separación de escalas; junto a estas aparecen determinadas estructuras jerárquicas, correlacionando las distintas escalas de un sistema. Estos conceptos expresan en el mundo instrumental las nociones de propiedades universales y clases de universalidad.
Merece la pena destacar que este reemplazamiento de las nociones de homogeneidad y separación de escalas por una concepción más orgánica (la auto-similaridad, conceptual y matemáticamente, permite conectar las diferentes escalas de un sistema) y dinámica (puesto que las estructuras fractales son estructuras recurrentes) ocurre también en la mecánica cuántica a la luz de las últimas investigaciones en dos sentidos: por un lado, en la inseparabilidad teórica y matemática de las fuerzas fundamentales (matemáticamente hablando, por ejemplo, no es posible integrar la función que las contiene para estimar la contribución individual que cada una de ellas en la versión cuántica de lo que en física clásica se conoce como momento de fuerza -que es a lo que se refiere Hegel cuando habla de los omentos de fuerza de la palanca, como se vio antes-); por otro lado, en relación a la homogeneidad del universo. Ambas cuestiones se abordarán de forma conjunta en la sección relativa al principio monista de complementariedad.
Además, esta posición frente a la homogeneidad perfecta no sólo se encuentra en la economía política marxista y la mecánica cuántica, también en las ciencias médicas. Así, señala (Sharma & Vijay, 2009, pág. 110) que en la evolución del endotelio[3], que partió de un vertebrado ancestral hace unos 540-510 millones de años y tenía como objetivo optimizar la dinámica del flujo y la función de barrera (y/o para localizar las funciones inmunes y de coagulación) fue decisivo (y los autores señalan que hay que ser enfáticos en eso) el hecho de que la heterogeneidad endotelial evolucionó como una característica central del endotelio desde el principio, lo que según los mismos autores refleja su papel en la satisfacción de las diversas necesidades de los tejidos corporales.
Las nociones antes expuestas sobre renormalización están íntimamente relacionadas con el concepto de estructura fractal. Según (Mandelbrot, 1983, pág. 15), quien acuñó el concepto, una estructura fractal es un conjunto para el cual la dimensión de Hausdorff-Besicovitch excede estrictamente la dimensión topológica. ¿Qué es una dimensión de Hausdorff-Besicovitch?, ¿qué es una dimensión fractal en general? Como se señala en (FOLDOC, 2021), una dimensión fractal puede definirse, a grandes rasgos, como la magnitud resultante de operar el límite del cociente del cambio logarítmico en el tamaño del objeto y el cambio logarítmico en la escala de medición, cuando la escala de medición se acerca a cero. Las diferencias entre tipos de dimensión fractal provienen de las diferencias en lo que se entiende exactamente por “tamaño del objeto” y lo que se entiende por “escala de medición”, así como por los diferentes caminos que es posible tomar para obtener un número promedio de muchas partes diferentes de un objeto geométrico. Como puede observarse, las dimensiones fractales cuantifican la geometría estática de un objeto.
(Lesne, Renormalization Methods, 1998, pág. 270) señala que las propiedades fractales de una estructura natural se definen solo aproximadamente, localmente y en un dominio de escalas que está acotado por arriba y por abajo. Además, generalmente son solo propiedades estadísticas, que se vuelven observables y bien definidas solo promediando sobre diferentes subdivisiones, para las cantidades globales como N(a,r) [4],o sobre diferentes centros para las cantidades locales como n(a,r,x ̅_0 ).
Como señala (Lesne, Renormalization Methods, 1998, pág. 265) , el hecho que la teoría sobre fractales aborde la mayor parte de temas que aborda la teoría de renormalización obedece a que los principios físicos que subyacen a la presencia de estructuras fractales son los mismos que hacen que los métodos de renormalización funcionen. Las nociones esenciales de leyes de escala y de invariancia de escala, de auto-similaridad y de universalidad aparecen en ambas situaciones. ¿Qué es una estructura fractal entonces? Es una representación visual de las características que asegura que los métodos de renormalización son relevantes para el análisis del sistema en el que aparece; la expresión de su auto-similaridad guía la elección del formalismo (metodológico) y la construcción subsiguiente del operador de renormalización. Las singularidades locales[5] de las medidas[6] fractales (análisis fractal de medidas de conjuntos, usualmente de la medida de Borel en R^d) pueden describirse jerárquicamente por su espectro dimensional[7], determinadas por el análisis multifractal[8] o reveladas por análisis de renormalización antes delineado.
A través del concepto de isomorfismo, originalmente perteneciente a la topología algebraica y expuesto anteriormente, pueden vincularse teórica y empíricamente:
- La teoría matemática de los sistemas complejos[9] (representada en las estructuras fractales auto-similares).
- Los sistemas disipativos[10].
- Los sistemas mecánico-cuánticos[11].
(Vitiello, 2014, pág. 203) establece que en electrodinámica existe un intercambio mutuo de energía y momento entre el campo de materia y el campo electromagnético, la energía total y el momento se conservan y, a partir de ello, muestra que para un fenómeno de tipo electromagnético conformado por un campo magnético constante y un potencial escalar armónico[12], el sistema electrodinámico que modela dicha clase de fenómenos es isomórfico (topológicamente equivalente) a un sistema de osciladores armónicos amortiguados/amplificados[13]. Estos pueden describirse mediante estados coherentes[14] comprimidos[15] que a su vez son isomorfos a estructuras fractales auto-similares. Bajo dichas condiciones de campo magnético constante y potencial escalar armónico, la electrodinámica es, por tanto, isomorfa a estructuras fractales auto-similares (que presentan alguna propiedad universal o clases de universalidad para estructuras discontinuas) y estados coherentes comprimidos. A nivel cuántico, la disipación induce una geometría no-conmutativa[16] con el parámetro de compresión[17] jugando un papel relevante.
La ubicuidad[18] de los fractales en la Naturaleza y la relevancia de los estados coherentes y la interacción electromagnética apuntan, según Vitiello, hacia “una visión unificada e integrada de la Naturaleza”; por supuesto, esta unificación e integración a la que se refiere el autor citado es fundamentalmente instrumental, no de carácter general como la aquí planteada. Un bosquejo sobre las razones por las que esta vinculación de carácter tan general es posible de establecer alrededor del ruido rosa se presenta a continuación.
Como señala (Zhao, 2021, pág. 2), las propiedades de un sistema físico pueden revelarse analizando sus respuestas frente a perturbaciones externas. La forma en que las respuestas de un sistema se pueden clasificar en varias categorías principales. Aquí hay algunos ejemplos:
En su investigación, Zhao estudia una clase de sistemas complicados (difícil a nivel su operativización) en cuanto son particularmente extendidos espacialmente (como arena apilada) y cuyas respuestas a pequeñas perturbaciones no tienen una longitud o un tiempo característicos. Las respuestas contienen una serie de eventos en toda la duración y escala de tiempo. Su distribución de probabilidad frente al tiempo o la duración obedece la ley de potencia[19], lo que significa que no hay un valor esperado de tiempo o duración de las respuestas. En particular, la distribución de probabilidad de la energía liberada en los eventos tiene la forma 1/f^α ,con α≈1, por lo que se denomina ruido “similar a 1 /f”, en donde 1/f es el conocido ruido rosa[20], que es el hecho empírico-instrumental alrededor del cual Vitiello fundamenta su enfoque formal integral de la Naturaleza. ¿Por qué ocurre esto?
Señala (Zhao, 2021, págs. 6-7) que la autoorganización crítica (SOC, de ahora en adelante) fue sugerida por Per Bak, Chao Tan y Kurt Wiesenfeld en 1987. El título del artículo era Self-Organized Criticality: An Explanation of 1/f noise. En este artículo, Bak et al. argumentaron (como característica distintiva de los sistemas SOC) que cuando un sistema extendido espacialmente con muchos grados de libertad es alejado del equilibrio por una fuerza externa, el estado estacionario es un estado con correlación espacial de ley de potencia.
Así, un sistema dinámico clásico evolucionará espontáneamente a un “estado crítico” que carece de una longitud característica. También argumentaron que la falta de una longitud característica provocará la falta de un tiempo característico, lo que inducirá un comportamiento de ley de potencia en el espectro de frecuencias (el que se señaló antes). En palabras del autor, “El mensaje más emocionante de este artículo es que hay sistemas que no necesitan un ajuste de parámetros, sino que evolucionan espontáneamente hasta un punto crítico.” (p. 7).
La idea original de Bak et al. es que:
- El concepto de SOC es universal: los sistemas espacialmente extendidos en la naturaleza siempre están en el estado SOC.
- SOC causa el espectro de potencia similar a 1/f. Estas ideas físicas básicas no son difíciles de comprender cuando consideramos modelos simples como un montón de arena o el modelo de Burridge-Knopoff[21]. Sin embargo, después de 18 años de investigaciones teóricas y experimentales, la gente todavía no tiene una comprensión clara del SOC. Primero, los experimentos y las simulaciones por computadora han demostrado que muchos sistemas están en el estado SOC solo bajo ciertas condiciones, lo que significa que no está garantizada la universalidad de los SOC afirmada por Bak et al. En segundo lugar, hay algunos sistemas que tienen las “huellas digitales” de SOC, pero tienen ruido 1/f^2 en lugar de un ruido no trivial similar a 1/f. Sin embargo, la idea de Bak et al. es valiosa en el sentido de que proporcionó a las personas una forma de resolver tales problemas en un marco teórico preestablecido, aunque es evidente la necesidad de continuar sobre esa ruta teórica la investigación científica sobre los sistemas autoorganizados.
A la luz de lo planteado en esta sección, puede establecerse, en relación al automovimiento general de la Naturaleza y la sociedad, que los componentes (modelados mediante ecuaciones) de una totalidad de referencia (modelada mediante un sistema de ecuaciones) comparten una esencia común (i.e., que son isomórficos entre sí) que permite su combinación integro-diferencial[22] de forma armónica y coherente bajo una determinada estructura interna de naturaleza material (objetiva), no-lineal (la totalidad es diferente a la suma de sus partes) y dinámica (el tiempo transcurre y el sistema, así como sus componentes, cambia) generada por la interacción de tales componentes bajo determinadas condiciones iniciales[23]. La estructura interna del sistema (o totalidad de referencia) condiciona a los componentes que la generan bajo el mismo conjunto de leyes (pero generalizado, por lo que no es formalmente el mismo) que rigen la interacción entre las condiciones iniciales y las relaciones primigenias entre componentes que determinaron la gestación de dicha estructura interna[24], [25]. Estas leyes son: 1. Unidad y Lucha de los Contrarios (que implica emergencia[26] y autoorganización[27] -al menos de tipo SOC-), 2. Salto de lo Cuantitativo a lo Cualitativo (implica emergencia, bifurcación[28] y salto[29]), 3. Ley de la Negación de la Negación (que es la crisálida del proceso dinámico antes descrito, en donde lo que negó es negado).
Lo anteriormente expuesto no debe resultar extraño, no en cuanto la complejidad misma posee un significado intrínsecamente dialéctico. Como señala (Moreno Ortiz, 2005, pág. 4), desde un punto de vista etimológico, la palabra “complejidad” es de origen latino, proviene de complectere, cuya raíz plectere significa ‘trenzar, enlazar’. El agregado del prefijo com- añade el sentido de la dualidad de dos elementos opuestos que se enlazan íntimamente, pero sin anular su dualidad. De allí que complectere se utilice tanto para referirse al combate entre dos guerreros, como al entrelazamiento de dos amantes.
Finalmente, con miras a reforzar la exposición realizada en esta sección sobre el amplio espectro de aplicación de los sistemas complejos (específicamente en términos del amplio espectro de surgimiento que poseen), señala (Lesne, Renormalization Methods, 1998, pág. 140) que la aparición de la noción de caos determinista fue la señal para el abandono de la idea básica establecida por Lev Landau (1944), según la cual las leyes de evolución deterministas y regulares generan un comportamiento asintótico caótico sólo después de la desestabilización de un número infinito de grados de libertad. La insuficiencia de esta teoría se reveló cuando se obtuvo evidencia de que las características caóticas pueden ocurrir en sistemas con solo un pequeño número de grados de libertad, o incluso en sistemas de dimensión infinita que involucran solo un subespacio de dimensión finita del espacio de fase. Un ejemplo de este segundo caso lo da un sistema espacio-temporal cuya dinámica se puede extender a un número finito de funciones espacio-temporales dadas, lo que reduce el estudio al del sistema dinámico que describe la evolución puramente temporal del número finito de coeficientes que ocurren en esta descomposición. La posibilidad del caos no está excluida a priori, excepto para evoluciones continuas autónomas en la dimensión 1 o 2.
Referencias
FOLDOC. (29 de 12 de 2021). Obtenido de Free On-Line Dictionary of Computing: https://foldoc.org/fractal+dimension
Frolov, I. T. (1984). Diccionario de filosofía. (O. Razinkov, Trad.) Moscú: Editorial Progreso. Obtenido de http://filosofia.org/
Fundación Gustavo Bueno. (29 de 12 de 2021). Conexión universal entre los fenómenos. Obtenido de Diccionario soviético de filosofía: https://www.filosofia.org/enc/ros/conex.htm
Lesne, A. (1998). Renormalization Methods. Critical Phenomena, Chaos, Fractal Structures. West Sussex, Inglaterra: John Wiley lk Sons Ltd,.
Lesne, A., & Laguës, M. (2012). Scale Invariance. From Phase Transitions to Turbulence (Primera edición, traducida del francés (que cuenta con dos ediciones) ed.). New York: Springer.
Mandelbrot, B. B. (1983). The Fractal Geometry of Nature. New York: W. H. Freeman and Company.
Moreno Ortiz, J. C. (2005). El Significado y el Desafío de la Complejidad para la Bioética. Revista Latinoamericana de Bioética, 1-19. Obtenido de https://www.redalyc.org/pdf/1270/127020937001.pdf
Rosental, M. M., & Iudin, P. F. (1971). DICCIONARIO FILOSÓFICO. San Salvador: Tecolut.
Sharma, & Vijay. (2009). Deterministic Chaos and Fractal Complexity in the Dynamics of Cardiovascular Behavior: Perspectives on a New Frontier. The Open Cardiovascular Medicine Journal, 110-123. Obtenido de https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2757669/pdf/TOCMJ-3-110.pdf
Vitiello, G. (2014). On the Isomorphism between Dissipative Systems, Fractal Self-Similarity and Electrodynamics. Toward an Integrated Vision of Nature. systems, 203-206.
Zhao, X. (30 de Diciembre de 2021). 1/f like noise and self organized criticality. Obtenido de University of Illinois at Urbana Champaign: https://guava.physics.uiuc.edu/~nigel/courses/563/Essays_2005/PDF/Xin.pdf
[1] Los umbrales son valores definidos que determinan si un estadístico (magnitud generada a partir de un conjunto de datos reales mediante algún modelo matemático-computacional que provee algún tipo de información sobre los datos usados) está por encima, por debajo o dentro de un rango normal en su red; la normalidad lo determina el curso de las investigaciones en el campo en el que se está realizando. Los umbrales también se utilizan al mostrar colores en paneles. Todo lo que esté por debajo del umbral marginal es azul, todo lo que esté entre el umbral marginal y el crítico es amarillo y todo lo que esté por encima del umbral crítico es rojo. Los umbrales también se pueden utilizar como parte de los widgets de estado que se basan en el rendimiento o en una línea de base. Véase https://observerdocs.viavisolutions.com/index.html#page/Observer_Apex/understanding_thresholds.html. El umbral es también conocido como límite termodinámico (para problemas espaciales) o régimen asintótico (para problemas temporales), en los que la aparición de singularidades marca un fenómeno crítico; en el estudio de los sistemas inestables, James Clerk Maxwell en 1873 fue el primero en utilizar el término singularidad en su sentido más general: aquel en el que se refiere a contextos en los que cambios arbitrariamente pequeños, normalmente impredecibles, pueden conducir a efectos arbitrariamente grandes (véase https://en.wikipedia.org/wiki/Singularity_(system_theory)).
[2] Se les dice “críticos” en cuanto exceden el umbral.
[3] Tejido formado por una sola capa de células que tapiza interiormente el corazón y otras cavidades internas.
[4] Una región centrada en a y con longitud característica r, siendo ésta última una medida que define la escala del sistema, por ejemplo, el radio en una circunferencia. A nivel de sistemas, la longitud característica se define como el volumen del sistema dividido sobre su superficie.
[5] Singularidades (en el sentido de Maxwell) que aplican únicamente en una región del espacio de interés o de referencia.
[6] Como señala (Kolmogórov & Fomin, 1978, pág. 290), el concepto de medida de un conjunto constituye una generalización natural de los siguientes conceptos: 1) de la longitud de un segmento, 2) del área de una figura plana, 3) del volumen de una figura en el espacio, 4) del incremento de una función no-decreciente en el semisegmento [a,b), 5) de la integral de una función no negativa en una región lineal, plana, del espacio, etc.
Retomando lo planteado en (Hegel F. , 1968, págs. 49-55), considérese un conjunto A con a elementos. Se dice que A está equipado con una medida M si una cierta medida M(E) es asignada a alguno de los subconjuntos E de A. El conjunto A, junto con su medida M, conforman un espacio métrico. La medida de un conjunto es un número real que es positivo o nulo. Además, la medida asume que si dos conjuntos no se intersecan (no tienen elementos en común) la medida de su suma es igual a la suma de sus medidas (es decir, la medida es lineal) y que la existencia de medidas de dos conjuntos implica la existencia de la medida de un tercer conjunto (que es igual a la medida de ambos conjuntos). La medida de todo el espacio de referencia, en el contexto de las probabilidades, es igual a 1. Un sistema de medidas es contablemente cerrado si contiene todas las posibles sumas contables de sus elementos. Finalmente, una medida es normal si para los conjuntos equipados de medida la condición E=∑E_n, E_n⋅E_m = 0, n ≠ m (n = 1, 2, …) implica M(E)=∑M(E_n); el enunciado anterior establece que cuando los subconjuntos E de A tengan entre sí una relación lineal perfecta (i.e., se nulifican al multiplicarse escalarmente) implica que la aplicación de la medida M sobre dichos subconjuntos será un procedimiento lineal (aplicarla al todo es equivalente a aplicarla a la suma de las partes).
[7] El vector característico o autovector de una transformación lineal (por ejemplo, la transformación lineal de un sistema de ecuaciones) es un vector no-nulo que cambia a lo sumo por un factor de escala (valor característico o autovalor) cuando la transformación lineal en cuestión es aplicada sobre el objeto matemático del que se trate. La generalización conceptual y matemática del conjunto de autovectores de una transformación lineal es conocida en el análisis funcional como espectro. Este espectro puede descomponerse en tres tipos de espectro, que conforman las partes del espectro en general: 1) espectro puntual (consistente en todos los autovalores del operador lineal de un espacio de Banach -espacio lineal X en que la región de convergencia de una sucesión de Cauchy pertenece a dicho espacio-, que es el operador que realiza la transformación lineal), 2) espectro continuo [que es el conjunto de escalares que no son autovalores, pero que hacen que la región conformada por las diferencias entre el operador lineal T y λ (donde λ es el conjunto de escalares que hacen que su diferencia con T no tenga una función inversa acotada -bien delimitada- en X)] sean un subconjunto propio (subconjunto que es igual al conjunto que lo contiene) y denso (un determinado subconjunto E es denso en un espacio X si todo elemento de X o pertenece a E o está arbitrariamente cerca de algún miembro de E) del espacio X, 3) espectro residual (todos los escalares del espectro que no son escalares puntuales ni continuos).
[8] Como señala (Lesne, Renormalization Methods, 1998, pág. 271), una de las tres estructuras fractales más complejas es aquellas que pertenecen a la familia de fractales superpuestos, donde la dimensión fractal local D(x) (que significa que la dimensión fractal pertenece a una subregión del espacio de interés centrada en x) depende de x de manera muy irregular: para cada valor D, {x,D (x)= D} es un conjunto fractal muy lacunar [un conjunto fractal lacunar es aquel en que la distribución de sus componentes -resultante de su patrón de iteración- deja huecos (Lesne, Renormalization Methods, 1998, pág. 266), tal como se puede observar al realizar iteraciones con el conjunto de Cantor (Lesne, Renormalization Methods, 1998, pág. 267)]. Establecido lo anterior, el análisis multifractal se diseñó con el fin de describir para cada valor de D su distribución fractal entrelazada en el espacio x.
[9] Conocida usualmente como teoría matemática del caos.
[10] En general, una estructura disipativa es aquella estructura coherente (en términos de su lógica interna) y autoorganizada (es un proceso en el que alguna forma global de orden o coordinación surge de las interacciones locales entre los componentes de un sistema inicialmente desordenado) que aparece en sistemas que se encuentran fuera del equilibrio (a menudo lejos del mismo) en un entorno con el que realiza intercambios de algún tipo. En física, estos sistemas son termodinámicos y los intercambios son en términos de materia y energía. Ilya Prigogine obtuvo en 1977 el Nobel de Química por el descubrimiento de los sistemas disipativos.
[11] Sistemas mecánicos de naturaleza física en que la inclusión del cuanto de acción es relevante; sobre el cuanto de acción se hablará en la sección correspondiente al principio monista de complementariedad.
[12] El potencial escalar de un oscilador armónico. Un potencial escalar describe la situación en la que la diferencia en las energías potenciales de un objeto físico en dos posiciones diferentes depende solo de las posiciones, no de la trayectoria tomada por el objeto al viajar de una posición a la otra. Un ejemplo son las diferencias en la energía potencial del objeto físico a causa de la gravedad (el diferencial energético sólo depende de la posición del objeto).
[13] Un oscilador armónico es en mecánica clásica un sistema que, cuando se desplaza de su posición de equilibrio, experimenta una fuerza restauradora F proporcional al desplazamiento x; algo similar a la lógica de la mano invisible de Smith, que matematizó Walras (aunque bajo un espíritu esencialmente diferente, en relación a las posibles perturbaciones que pudiese sufrir el sistema económico de su posición de equilibrio (donde la oferta y la demanda se igualan, para el caso neoclásico). Un oscilador armónico amortiguado es aquel oscilador armónico bajo la acción de una fuerza de amortiguación (fricción) proporcional a la velocidad del sistema (la velocidad de su trayectoria o tasa de crecimiento). Un oscilador armónico es también un sistema en el que un objeto vibra (que es la forma que adopta el movimiento en los sistemas de sonido) con cierta amplitud y frecuencia; en un oscilador armónico simple, no existen fuerzas externas como la fricción o las fuerzas impulsoras que actúan sobre el objeto o, en su defecto, su efecto es despreciable; por lo tanto, la amplitud y la frecuencia siempre son las mismas. En una oscilación armónica amortiguada existen fuerzas (fricción) que actúan sobre el objeto, lo que tiene el efecto de que la amplitud (de la trayectoria) disminuya hasta que se detiene. En la vida real, la situación ideal de un oscilador armónico simple no existe. Esto significa que para mantener una oscilación debe aplicarse una fuerza impulsora o directora (conductora), de ahí el concepto de oscilador armónico dirigido.
[14] Un oscilador armónico cuántico es el análogo de un oscilador armónico clásico en la mecánica cuántica.
[15] Estado cuántico generalmente descrito mediante dos cantidades físicas mesurables no-conmutativas (véase la siguiente nota al pie) que tienen espectros continuos de autovalores.
[16] Una geometría no-conmutativa son espacios que presentan a nivel local (de una región de sí) estructuras algebraicas no-conmutativas, que son estructuras matemáticas en que uno de los operadores (símbolo que indica que se realiza una operación) binarios (porque la operación es efectuada sobre dos elementos) principales no cumple con la propiedad conmutativa al relacionar cualesquiera dos pares de elementos que se encuentren dentro de dicha localidad. Esto puede extenderse a estructuras usuales como la topología de un espacio o la norma del mismo y, conceptualmente, significa que la disipación, a nivel cuántico, induce una geometría en que el orden resulta relevante para una de las relaciones fundamentales que describen la operación de un determinado sistema en una región definida del espacio.
[17] Un parámetro es, conceptualmente hablando, una variable que sirve para identificar los elementos (usualmente funciones) que pertenecen a una determinada familia (que es una forma más general de conjunto). Comprendido esto, ¿qué es luz comprimida (del inglés squeezed light)? Señala (Lvovsky, Squeezed light, 2015, pág. 121) que la luz comprimida es un estado físico de la luz en el cual el ruido de un campo eléctrico en ciertas fases cae por debajo del estado de vacío (estado cuántico con la menor energía posible). Esto significa que, cuando se enciende la luz comprimida, se detecta menos ruido que en el caso que no hubiese ninguna luz. Esta característica aparentemente paradójica es una consecuencia directa de la naturaleza cuántica de la luz y no puede explicarse dentro de la mecánica clásica (bajo la lógica clásica es que resulta paradójica, aunque no lo sea). Comprendido lo anterior, resulta natural comprender el parámetro de comprensión lumínica como la variable que permite identificar como pertenecientes a una determinada familia de estados físicos a todas las funciones que modelan estados de luz comprimida. Como se señala en (Lvovsky, Squeezed light, 2015, pág. 128) y en (Lvovsky, Squeezed light, 2016, pág. 4), si un estado de comprensión cuántica de la luz se modela mediante la identidad S ̂(r)=exp[(ζa ̂-ζa ̂^(†2) )/2, en donde a ̂ es el operador de aniquilación y a ̂^(†2) es el operador de creación, entonces su parámetro de comprensión se expresa mediante ζ=re^iϕ, donde r es igual al logaritmo natural del factor de compresión r=ln(R), i es la coordenada rotacional (imaginaria) y ϕ son números reales (la fase ϕ determina el ángulo de la cuadratura que se comprime). Como señala (Drummond & Ficek, 2004, págs. 14-15), las propiedades estadístico-cuánticas de los estados coherentes están completamente determinadas por los valores medios de los operadores de posición y momento y sus varianzas. Complementariamente a lo anterior, señala que los estados comprimidos de radiación se producen en procesos no-lineales en los que un campo electromagnético “clásico” impulsa un medio no-lineal. En el medio no-lineal, se pueden generar pares de fotones correlacionados de la misma frecuencia. Un operador de compresión (una fuerza con las características necesarias para comprimir en la forma cuántica antes descrita la luz) puede aplicarse sobre estados coherentes y producir estados coherentes comprimidos (los estados coherentes de un oscilador armónico son aquellos que tienen la característica que sus valores esperados observables evolucionan de la misma forma en que lo hace un sistema dinámico clásico).
[18] La ubicuidad, como cualidad de ubicuo, es la característica de un ente de estar presente a un mismo tiempo en todas partes.
[19] Ley estadística que establece la relación funcional entre dos cantidades, donde un cambio relativo en una cantidad da como resultado un cambio relativo proporcional en la otra cantidad, con independencia del tamaño inicial de esas cantidades. Lo anterior equivale a afirmar que una cantidad varía como potencia de otra.
[20] Como señala (Mandelbrot, 1983, pág. 74), en física el ruido es sinónimo de posibilidad de fluctuación o error, independientemente de su origen y manifestación. Por otro lado, señala (Kiely, 2021, pág. 1) que el ruido 1/f es un ruido de baja frecuencia para el que la potencia del ruido es inversamente proporcional a la frecuencia. El ruido 1/f se ha observado no solo en la electrónica, sino también en la música, la biología e incluso la economía. Las fuentes del ruido 1/f todavía se debaten ampliamente y aún se están realizando muchas investigaciones en esta área.
[21] El modelo de Burridge-Knopoff es un sistema de ecuaciones diferenciales utilizado para modelar terremotos usando n puntos en línea recta, cada uno de masa m, que interactúan entre sí a través de resortes, y en el que todas las masas están sujetas a una fuerza que es proporcional a las distancias x_i(t) de las masas desde su posición de equilibrio y hasta una fuerza de fricción F(v), donde v es la velocidad.
[22] Es decir, que permite la acción de leyes integrales o leyes diferenciales según corresponda.
[23] Que inexorablemente, como indicaba Levins al validar el argumento de Engels, implica las condiciones iniciales no solo del sistema analizado en sí mismo sino también las del entorno.
[24] La estructura interna del sistema, lo que filosóficamente es esencia y matemáticamente es su topología.
[25] Así se establece que el todo, generado por las partes en el estado inicial, ulteriormente se vuelve más que las partes, adquiere independencia relativa de estas y las determina; por supuesto, las partes también influyen en el todo y lo modifican (aunque, evidentemente, la influencia no es tan condicionante en el sentido inverso, al menos no como caso general; las excepciones obedecen a condiciones concretas del momento de desarrollo del todo analizado y, en última instancia, la acción de las partes ha sido determinada de forma mediata -histórica, acumulativa- o bien, para el caso de los componentes genéticos del todo analizado -sus componentes históricamente primigenios-, las partes fueron condicionadas en el momento de formación del todo por las condiciones bajo las cuales tales partes se relacionaron de forma combinatoria (el contexto de formación del sistema estudiado), así como también cada una de estas partes es la cristalización de la dinámica acaecida en otros sistemas, en sus sistemas de referencia), de ahí que la independencia del todo respecto a estas sea relativa, no absoluta.
[26] Cualidad de los sistemas de transitar de una estructura simple hacia estructuras más complejas (sistemas en que la totalidad no puede ser reducida a la suma de sus partes).
[27] A grandes rasgos, puede definirse como aquel proceso en el que alguna forma de orden general surge de interacciones locales entre partes de un sistema inicialmente desordenado. La autoorganización crítica es una forma laxa de autoorganización (más general, en cuanto relaja los requerimientos).
[28] Como señala (Weisstein, 2021), una bifurcación es una separación de la estructura sistémica en dos ramas o partes. En sistemas dinámicos es una duplicación, triplicación, etc., que acompaña al inicio del caos. Una bifurcación representa una súbita apariencia de cambio cualitativo en relación a las soluciones del sistema no-lineal cuando algunos parámetros varían.
[29] En su sentido cuántico, un salto es la transición abrupta de un sistema cuántico de un estado a otro (o de un nivel de energía a otro); el término “salto” tiene como finalidad distinguirlo de los sistemas clásicos, en los cuales las transiciones son graduales. En un sentido dialéctico-materialista, un salto es un concepto más amplio que el de la mecánica cuántica y la mecánica clásica considerados aisladamente, que se asimila más al mecanismo evolutivo de Darwin-Gould: Charles Darwin estableció que la evolución por diferenciación y selección actuaba gradualmente, mientras que el biólogo marxista Stephen Jay Gould complementó esto afirmando que en algunos contextos podían ocurrir saltos abruptos (esto se expandirá más adelante cuando se analicen los equilibrios puntuados de Gould). Un salto, en su sentido dialéctico-materialista es, muy sintéticamente, la solución de la continuidad, la transición rápida y súbita de una cualidad a otra, gracias a la acumulación paulatina de los cambios cuantitativos insignificantes e imperceptibles (Fundación Gustavo Bueno, 2021).